§ 3 equal-parameter units and higher-order interpolation
1.
Equal parameter unit
If the unit has the following properties:
(i)
Each undetermined function ( eg u ) has only one parameter value on the node ( ie ); when the coordinate value of the node ( eg ) is regarded as the parameter value of the coordinate variable ( eg x ) on the node , each on the element The node parameter values of the undetermined function and the coordinate variable have the same number , that is, the number of nodes p .![]()
![]()
![]()
![]()
![]()
(ii)
The linear relationship between the coordinates of the change point P on the element and each component of the interpolation function and the node parameter value has a uniform pattern:
![]() ( 14 )
( 14 )
It is called an equal parameter unit. In the formula, it is a type function with local coordinates as variables , ( * ) represents the coordinate of the change point P or each component of the interpolation function , and represents the corresponding node parameter value. Basic elements are the simplest class of isoparametric elements ( only vertices are nodes ) .![]()
![]()
If the nodes are not only taken at the vertices , the number of times that the definition and composition of the function can be known will increase , and the number of interpolation functions will also increase accordingly. Conversely , in order to improve the accuracy, the function to be determined must be interpolated with higher order, and the nodes of the element cannot be taken only at the vertices . In short , isoparametric elements are suitable for high-order interpolation , and the key is still the composition of the type function. The transformation of the element into a regular shape is not necessarily achieved by metric ratio coordinates , as long as the local coordinates of its nodes are selected to make the type function expression concise. All right. As for the correspondence between the local coordinates and the Cartesian coordinates, the above model can be used. Common types of isoparametric elements include six-node triangle , nine- and ten-node triangle , eight- and nine-node quadrilateral , ten-node tetrahedron , twenty-node tetrahedron , fifteen-node pentahedron , and twenty-node hexahedron.![]()
In order to unify the formula , for triangles and tetrahedrons , it is necessary to simplify the node notation : first, like the basic element , only the local number i = 1 , 2 , ..., p at the vertices of the element , and directly use i to represent the vertices of the element , with Represents the midpoint of the line segment whose endpoint is , and represents the third point on the line segment close to and respectively , to represent the centroid ( center of gravity ) of △ , and O represents the centroid of the element. None of them are additionally numbered during unit analysis . In addition , in order to shorten the length , only the expression of the type function is listed in the equivalent parameter unit , and the rest can be modeled on § 2![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() calculate.
calculate.
2. Interpolation on multi-node line elements
[ Three-node line element ] Take the midpoint of the straight line segment as another node , and its distance coordinate is . The corresponding type function is quadratic:![]()
![]()
![]()
![]()
![]()
![]()
![]()
The interpolation function is
![]()
Using the original Cartesian coordinates, the interpolation function can be written as
![]()
It is the quadratic Lagrangian interpolation polynomial of u ( x ) , where .![]()
[ Four-node line element ] Take the three-point point on the straight line segment as the other two nodes , , and the distance coordinates are respectively , , and the corresponding type function is cubic:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The cubic Lagrangian interpolation polynomial u ( x ) can be obtained using the original Cartesian coordinates :

in the formula
![]()
![]()
3. The type function of plane and other parametric elements
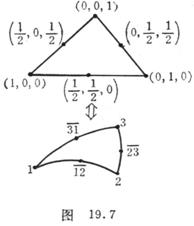
[ Six-node triangle ] A six-node consists of the three vertices of the triangle and the midpoints of the three sides ( Figure 19.7 ). Choose area coordinates , whose type function is quadratic:![]()
![]() ( i = 1,2,3 )
( i = 1,2,3 )
![]() ( i ≠ j )
( i ≠ j )
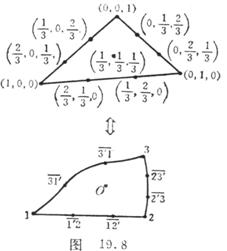
[ Nine and ten-node triangles ] The nine-nodes include the three vertices of the triangle and the thirds of the three sides ; the ten-nodes should be supplemented with the centroid O of the element ( Figure 19.8), and its area coordinates are .![]()
The form function for a ten-node triangle is cubic:
![]() ( i = 1 , 2 , 3 )
( i = 1 , 2 , 3 )
![]() ( i ≠ j )
( i ≠ j )
![]()
For a nine-node triangle , each undetermined function has only 9 degrees of freedom node parameter values , and the 10 coefficients in the impossible cubic homogeneous formula can be formed but not unique. For example, refer to the above formula to take![]()
![]() ( i = 1 , 2 , 3 )
( i = 1 , 2 , 3 )
![]() ( i ≠ j )
( i ≠ j )
As long as it is clear that both of them can be used as type functions , but the resulting cubic interpolation is not complete , for which it is necessary to![]()
 type function or interpolation function. It can be shown that the corresponding interpolation then contains a complete quadratic polynomial ( cf. § 4 ) . So the form function of a nine-node triangle can be written as
type function or interpolation function. It can be shown that the corresponding interpolation then contains a complete quadratic polynomial ( cf. § 4 ) . So the form function of a nine-node triangle can be written as![]()
![]() ( i = 1 , 2 , 3 )
( i = 1 , 2 , 3 )
![]() ( i ≠ j )
( i ≠ j )
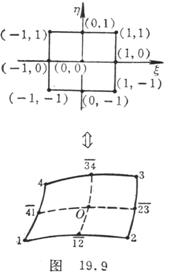
[ Eight and nine-node quadrilateral ] The eight-node includes the four vertices of the quadrilateral and the midpoint of the four sides , and the nine-node should add the centroid of the element . Consider first the square in local coordinates , centered at the origin , its vertex coordinates , etc. ( Fig. 19.9 ) .![]()
![]()
The form function of the nine-node quadrilateral is
![]() ( i = 1,2,3,4 )
( i = 1,2,3,4 )
![]() ( i ≠ j )
( i ≠ j )
![]()
The form function of an eight-node quadrilateral is
![]() ( i = 1,2,3,4 )
( i = 1,2,3,4 )
![]() ( i ≠ j )
( i ≠ j )
Fourth,
the type function of parameters such as space
[ Ten-noded tetrahedron ] Ten-noded tetrahedron consists of four vertices and midpoints of six edges ( Figure 19.10 ) . Select volume coordinates , and its type function is
![]() ( i = 1,2,3,4 )
( i = 1,2,3,4 )
![]() ( i ≠ j )
( i ≠ j )
[ Twenty-noded tetrahedron ] Twenty-nodes include the four vertices of the tetrahedron, the three-points of the six edges ( ![]() 12 in total ) , and the centroids of the four boundary surfaces ( such as 4 in total ) ( Fig. 19.11 ) . Its type function is:
12 in total ) , and the centroids of the four boundary surfaces ( such as 4 in total ) ( Fig. 19.11 ) . Its type function is:![]()
![]() ( i = 1,2,3,4 )
( i = 1,2,3,4 )
![]() ( i ≠ j )
( i ≠ j )
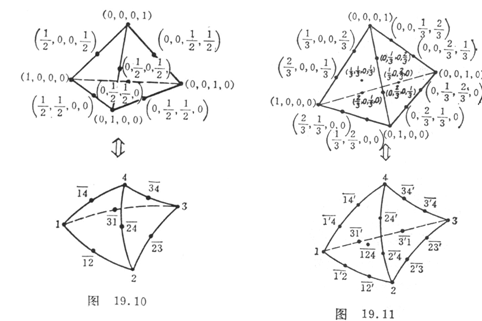
![]() ( i ≠ j ≠ k )
( i ≠ j ≠ k )
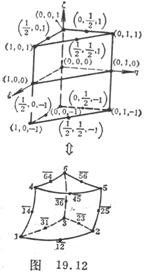
[ Fifteen node pentahedron ]
The fifteen nodes include the six vertices of the pentahedron , the midpoints of the three edges and the midpoints of the six sides of the upper and lower bases ( Figure 19.12 )
Its type function is

![]()
( j represents the midpoint of the triangular edge )
![]()
[ Twenty-noded hexahedron ]
The twenty-noded hexahedron consists of eight vertices and the midpoints of twelve edges ( Figure 19.13) . Its type function is
![]() ( i =1 ,2 ,…,8)
( i =1 ,2 ,…,8)
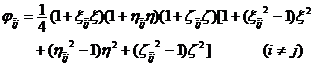
5. Characteristics of isoparametric units
Based on the above, it can be seen that the isoparameter unit has the following characteristics:
1°
Using equal-parameter elements has better effect than basic elements : it can not only increase the number of interpolations to improve the calculation accuracy , but also make the element shape adapt to the characteristics of boundary curvature. Because in the construction of the type function , we take the regular geometric elements in the local coordinate system as the model , and then give the corresponding relationship between the two nodes , and after the type function is obtained , we can obtain the two coordinate system through the mode ( 14 ) . relationship between. The boundary shape of the element is not considered in the whole process , but it can be seen from these relations that the boundary of the element can generally be substituted for a curve or surface.![]()
For example , the boundary of a ten-node triangle (x =0) can be a cubic curve. The edges of the ten-node tetrahedron, fifteen-node pentahedron or twenty-node hexahedron ( some two local coordinates have been determined ) are all quadratic curves , and the sides are surfaces woven by two families of quadratic algebraic curves. Its shape is completely determined by the node's position or coordinates ( ). If the nodes are chosen to be colinear or coplanar , it is not difficult to prove from mode ( 14 ) that these curves degenerate into straight or planar curves. Therefore, when dividing equal-parameter elements , some nodes adjacent to the curved boundary of Ω can be appropriately arranged to make the element fit the boundary of Ω well , so as to reduce the boundary disturbance error. But inside the area , it is better to choose the node to make the side face more straight (even as far as possible to be consistent with the direction of the Cartesian coordinate) , which can simplify the coordinate transformation and its Jacobian , so as to reduce the amount of calculation and the accumulation of errors.![]()
![]()
The number of terms of a 2°
-complete m -element n -degree polynomial or m + 1 -element n -degree homogeneous polynomial is the number of terms. This formula is useful for determining whether the compatibility condition is satisfied , whether the n -th degree interpolation is complete , and the reasonable distribution of nodes on the boundary. For example , the coordinate transformations of the above parameters such as planes are compatible on the boundary ; the quadratic and cubic interpolations of the ten-node and twenty-node tetrahedra are complete, and the elements are also compatible along the boundary sides. As for other elements , they are also compatible with some restrictions on the form of the interpolation function (eg requiring biquadratic).![]()
3° It can be known from the model ( 14 ) that the compatibility of coordinate transformation between equal parameter units is equivalent to the continuity of the interpolation function. If the number of node parameter values on the boundary is equal to the number of terms of the interpolation polynomial, the value of the interpolation function of two adjacent elements on the common boundary can usually be uniquely determined by their common node parameter values , and the continuity is guaranteed . In the same way , the parameter expressions of the coordinates on the common boundary are also completely determined by the coordinate values of its nodes , so that their coordinate transformations are kept compatible on the boundary. For example , from the type function of the twenty-node hexahedron, it can be seen that its interpolation polynomial includes ξ , η , ζ cubic polynomial 17 terms (that is, the 20th term does not appear in the third-order term) and then adds three quartic terms , for any one For a side (eg ζ = 1 ) , the interpolation function (pair ξ , η ) is biquadratic with a total of 8 terms , equal to the number of nodes (parameter values) on that side. therefore![]()
![]() , as long as the adjacent units adopt the same interpolation mode , the compatibility condition is satisfied. Note that increasing the number of nodes (parameter values) can only increase the degree of the interpolation polynomial to a certain extent , but cannot solve the problem that its derivatives remain continuous along the common boundary . For such problems, it is not appropriate to use equal-parameter units . Use the coordinating unit .
, as long as the adjacent units adopt the same interpolation mode , the compatibility condition is satisfied. Note that increasing the number of nodes (parameter values) can only increase the degree of the interpolation polynomial to a certain extent , but cannot solve the problem that its derivatives remain continuous along the common boundary . For such problems, it is not appropriate to use equal-parameter units . Use the coordinating unit .
4° It can be seen from the composition of the shape function of the nine- and ten-node triangular elements that if the interpolation function is not restricted , it is not unique . For example , for a fifteen-node pentahedron or a twenty-node hexahedron , three parallel The plane ζ = ζ +1 = ζ - 1 = 0 can pass through all nodes. This means adding the cubic term of ζ to the prototype function { } , ![]()
![]() as long as = 0 it is still a set of type functions. The restriction of the twenty-node hexahedron element on the interpolation polynomial has been described in 3 o (that is, the three terms in the cubic polynomial are removed , and only three terms are added in the fifteen quartic terms : ) , in this restriction (that is, for each All coordinate variables are quadratic) , the type function is unique (for example , since the cubic term of ζ does not appear , it can only be zero). same
as long as = 0 it is still a set of type functions. The restriction of the twenty-node hexahedron element on the interpolation polynomial has been described in 3 o (that is, the three terms in the cubic polynomial are removed , and only three terms are added in the fifteen quartic terms : ) , in this restriction (that is, for each All coordinate variables are quadratic) , the type function is unique (for example , since the cubic term of ζ does not appear , it can only be zero). same![]()
![]()
![]()
![]() , In the form function expression of the 15-node pentahedron element , , ,
, In the form function expression of the 15-node pentahedron element , , , ![]()
![]() etc. five cubic terms do not appear . Under such conditions , the form function is also unique.
etc. five cubic terms do not appear . Under such conditions , the form function is also unique.
The 5° incomplete high-order interpolation is generally detrimental to the convergence of the solution. However , as with the nine-node triangle , the above-mentioned interpolations for the twenty-node hexahedron and fifteen-node pentahedron elements are accurate for quadratic polynomials (since they only adjust for terms above the third degree).