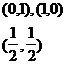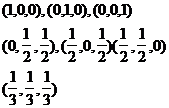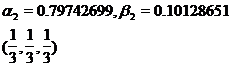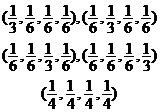Appendix Numerical Integration in Finite Element Method  

 

In element analysis, a large number of numerical integrals need to be calculated, and these integrals often transform the integrand (including the differential operator matrix B to the global Cartesian coordinates ) into functions of local coordinates by coordinate transformation, and most of them are about local coordinates. polynomial. For boxing, it can be transformed into the integral of the power function of the coordinate variables x , h , z , and for triangulation, it can be transformed into the integral of the power function of natural coordinates, and they are not difficult to integrate. The relevant formulas are listed below. For integrals whose integrand is not a polynomial, a Gaussian quadrature formula is needed to find its approximation. For the numerical integration of functions of local coordinates ( x , h , z ), please refer to Chapter 6, here only the Gaussian numerical integration table of functions of natural coordinates is listed.

[ Line segment unit ]

1°   Integral formula with distance coordinates  

Because , combined with the above formula, the included integral formula can be obtained.

2°   Commonly used numerical integration table  

The number of integration nodes m	Integrate Node Coordinates	Multiplying coefficient	Algebraic Accuracy * n
1		1	1
2	( α , 1 ),(1 , α ) where α = 0.2113248654		3
3			3
3	( α , 1 ),(1 , α ) where α = 0.1127016654		5

[ Triangular element ]

1°     Integral formula with area coordinates 

where A is the area of ​​the unit. It can be seen from the integral formula ( 2 ) of the coefficient matrix that the integrand not only includes the type function whose area coordinate is a variable, but also has a differential operator B about x and y . According to the matrix coordinate transformation

                             

Combined with the above formula , the integral formula can be obtained.

Note that if any side of the triangular element (for example ) is used as a line element, the above integral formula with distance coordinates also holds.

2°     Commonly used numerical integration table  

The number of integration nodes m	Integrate Node Coordinates	Multiplying coefficient	Algebraic accuracy n
1		1	1
3			2
7			3
7	in in	0.13239415       0.12593918       0.225	5

[ Tetrahedral unit ]

1°     Integral formula with volume coordinates  

where V is the volume of the unit. Formula ( 2 ) appears , that is, the integrand contains the derivative of the function with respect to x, y, z , according to the coordinate transformation

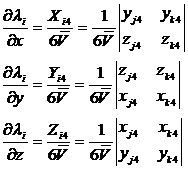
                             ( i =1 ,2,3 )

Combined with the above formula, the integral formula containing these partial derivatives can be obtained

2°     Commonly used numerical integration table

The number of integration nodes m	Integrate Node Coordinates	Multiplying coefficient	Algebraic accuracy n
1		1	1
4	in		2
5			3