Chapter 2 Calculation and Drawing of Elementary Geometric Figures

Chapter 2 Calculation and Drawing of Elementary Geometric Figures

Geometric figures are abstracted from the real world, so the theory, calculation and drawing of geometric figures are widely used in people's social practice .

This chapter focuses on two types of commonly used geometric figures: one is plane figures, such as triangles, quadrilaterals, regular polygons and various figures related to circles; the other is spatial three-dimensional figures, such as cubes, cuboids, spheres, cones, cylinders And various regular polyhedrons . The calculation formulas of their area, volume, side area, surface area, center of gravity and moment of inertia are collected in more detail here .

In addition, the drawing methods of some figures (such as regular polygons) are also introduced, and the ellipse drawing method and the arc lofting method commonly used in production practice are also briefly explained . The so-called "three major problems of geometry" that have been strictly proved cannot be drawn with rulers and compass .

§ 1 Triangles and quadrilaterals

First, the calculation of the elements of the triangle

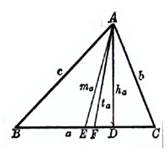
1. Elements of a triangle

Figure 2.1 Figure 2.2

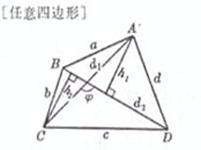
a, b, c are the three sides of the triangle and R is the radius of the circumcircle

A , B, C are the three angles r is the radius of the inscribed circle

AD is the height on the a side and H is the vertical center (the intersection of the three heights)

AF is the bisector of angle A and G is the center of gravity (the intersection of the three medians)

AE is the center line on the side of a (the intersection of the three angle bisectors)

is the half perimeter as the circumcentre (the intersection of three perpendicular bisectors)

S is the area of

2. Calculation formula of each element of triangle

[ high ]

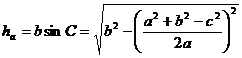
[ midline ]

[ angular bisector ]

[ area ]

[ Circumscribed circle radius ]

[ Inscribed circle radius ]

2. Calculation formulas for the area, geometric center of gravity, and moment of inertia of triangles and quadrilaterals

graphics

Area S , geometric center of gravity G and moment of inertia * J

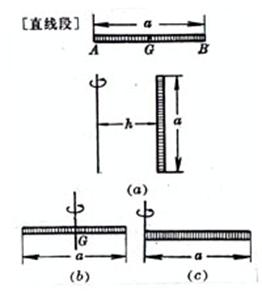
length L=a

Center of gravity GA=GB =

Moment of inertia

(a) The axis of rotation is parallel to the thin rod, and the distance to the thin rod

is h( figure ( a ))

(b) The rotating shaft passes through the center of gravity G of the thin rod ,and is connected to the thin rod

vertical ( figure ( b ))

(c) The axis of rotation passes through one end of the thin rod,and is connected to

Rod vertical ( figure ( c ))

In the table, m is the mass of the object, and the objects are all homogeneous . For the calculation formula of the moment of inertia of general objects, see Chapter 6,

§ 3 , 5 .

graphics

Area S , geometric center of gravity G and moment of inertia J

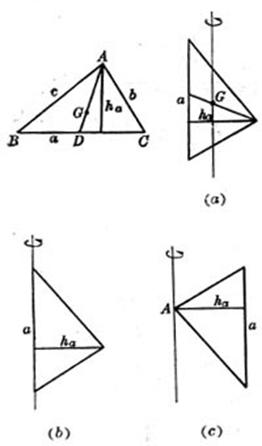
[ arbitrary triangle ]

a,b,c are three sides , the height on the side of a

[ isosceles triangle ]

b is the waist , a is the bottom edge , and a is the height on the side of a

center of gravity

Moment of inertia

( a ) The axis of rotation passes through the center of gravity G and is parallel to side a

( Figure ( a ))

( b ) the axis of rotation coincides with the side a of the triangle ( figure ( b ))

( c ) the axis of rotation passes through a vertex A of the triangle and is parallel to side a ( figure ( c ))

center of gravity

Moment of inertia

The shaft coincides with the height on the bottom edge

when a =b

graphics

Area S , geometric center of gravity G and moment of inertia J

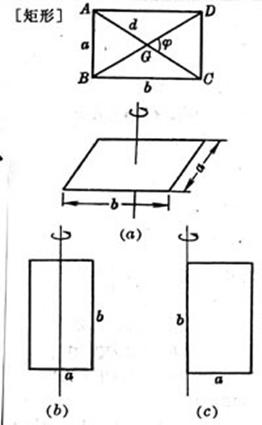
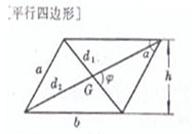
a, b are adjacent sides , d is the diagonal , and the included angle of the diagonal

a is the length of the side , the top angle , and the two diagonals

area

The center of gravity G is at the intersection of the diagonals , i.e.

Moment of inertia

( a ) The axis of rotation passes through the center of the rectangle and is perpendicular to the plane where the rectangle is located ( Figure ( a ))

( b ) The axis of rotation passes through the center of the rectangle and is parallel to the b side of the rectangle ( Figure ( b ))

( c ) The axis of rotation coincides with the b side of the rectangle ( Figure ( c ))

area

The center of gravity G is at the intersection of the diagonals , i.e.

Moment of inertia

( a ) The axis of rotation coincides with the diagonal ( Fig. ( a ))

( b ) The rotation axis passes through the center of gravity G and is perpendicular to the plane where the figure is located ( Figure ( b ))

graphics

Area S , geometric center of gravity G and moment of inertia J

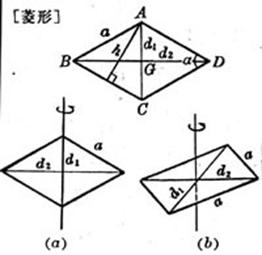
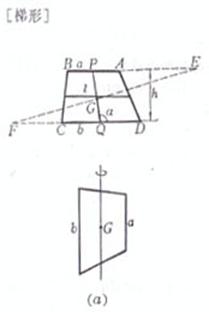
a, b are the adjacent sides , h is the distance between the opposite sides , is the top angle , is the two diagonals , is the angle between the two diagonals