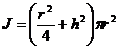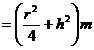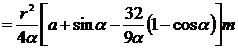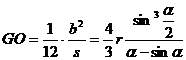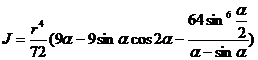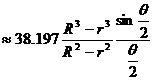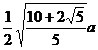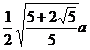§ 2 Circles and Regular Polygons
1.
Calculation formulas of various quantities related to circles
|
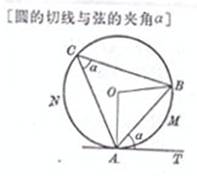
where represents the angle of the central angle ∠ AOB corresponding to the AMB arc (the same below), and C is any point on the ANB arc .
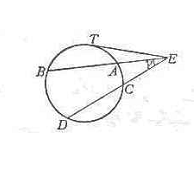
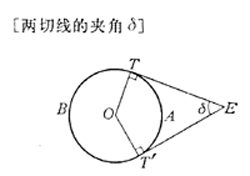
[ Two secant lines and their included angle ]
AE · BE=CE · DE=ET 2 |
AE · BE= CE · DE=r 2 -OE 2 where r is the radius of the circle .
|
|
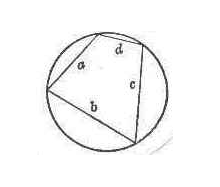
[ Area S of a quadrilateral inscribed in a circle ]
in the formula a,b,c,d are four sides |
|
2.
Calculation formulas for the area, geometric center of gravity and moment of inertia of various figures related to circles
|
graphics |
Area, Geometric Center of Gravity, and Moment of Inertia |
|
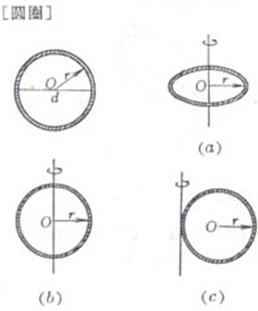
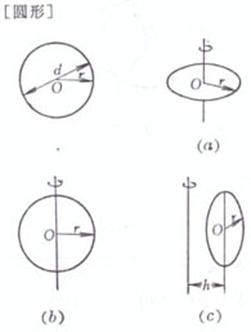
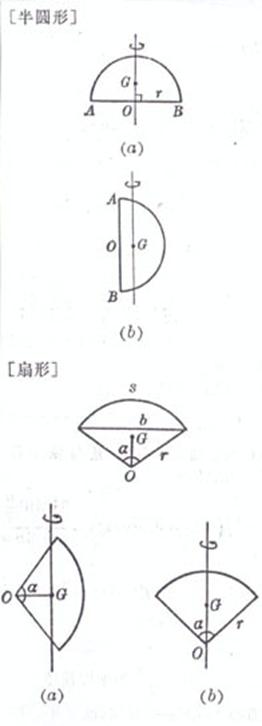
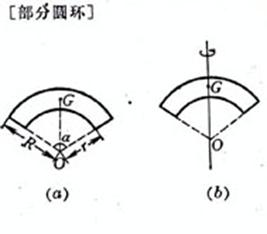
O is the center of the circle , r is the radius , and d is the diameter
O is the center of the circle , r is the radius , and d is the diameter |
perimeter The center of gravity G coincides with the center O of the circle Moment of inertia ( a ) The axis of rotation passes through the center of the circle and is perpendicular to the plane of the circle ( Figure ( a )) ( b ) The axis of rotation coincides with the diameter of the circle ( Figure ( b )) ( c ) The axis of rotation is a tangent to the circle ( Figure ( c )) area The center of gravity G coincides with the center O of the circle Moment of inertia ( a ) The axis of rotation passes through the center of the circle and is perpendicular to the plane of the circle ( Figure ( a )) ( b ) The axis of rotation coincides with the diameter of the circle ( Figure ( b )) ( c ) The axis of rotation is parallel to a certain diameter of the circle , and its distance is h ( Fig. ( c ))
|
|
graphics |
Area, Geometric Center of Gravity, and Moment of Inertia |
|
r is the radius , b is the chord length , is |
area center of gravity Moment of inertia (a)
The axis of rotation coincideswith GO (Fig.( a )) (b)
The axis of rotation passes throughpoint G andis parallel to the diameter AB (Fig.( b )) arc length area center of gravity
Moment of inertia (a)
The axis of rotation passes through point G on the graphics planeandis perpendicular to GO (Fig.( a ))
(b)
The axis of rotation coincideswith GO (Fig.( b ))
( At that time , it was a quarter circle ) |
|
graphics |
Area, Geometric Center of Gravity, and Moment of Inertia |
|
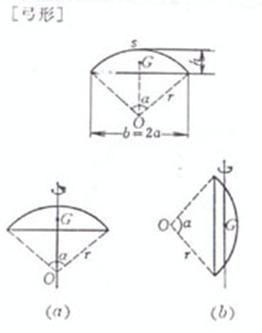
r is the radius , b is the chord length ( b=2a ), h is the arch height ,
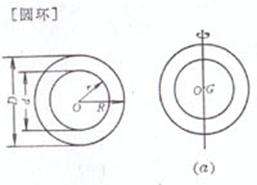
R is the outer radius , r is the inner radius , D is the outer diameter , d is the inner diameter , and O is the center of the circle |
Chord length vault area
center of gravity ( At that time , the bow was a semicircle ) Moment of inertia (a)
The axis of rotation coincideswith GO (Fig.( a )) (b)
The axis of rotation passes through the center of gravity G andis parallel to the chord(Fig.( b ))
area where t=Rr is the ring width ,
The center of gravity G coincides with the center O of the circle Moment of inertia The axis of rotation is on the graphics plane and passes through point G ( Figure ( a ))
|
|
graphics |
Area, Geometric Center of Gravity, and Moment of Inertia |
||||||||
|
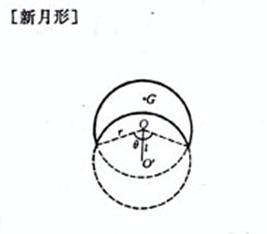
r is the radius , d is the diameter , l is the distance from the center of the circle , , is the opening angle |
area
center of gravity
The moment of inertia axis coincides with GO ( Fig. ( a )) area
in the formula center of gravity |
||||||||
|
|
0.1 |
0.2 |
0.3 |
0.4 |
|||||
|
|
0.399 |
0.795 |
1.182 |
1.556 |
|||||
|
|
|||||||||
|
|
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
||||
|
|
1.913 |
2.247 |
2.551 |
2.815 |
3.024 |
||||
|
|
|||||||||
3.
Conversion formulas and proportional coefficients of regular polygons
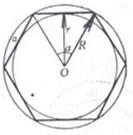
n is the number of sides R is the radius of the circumcircle
 a is the side length r is the radius of the inscribed circle
a is the side length r is the radius of the inscribed circle
![]() is the central angle S is the area of the polygon
is the central angle S is the area of the polygon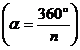
The center of gravity G coincides with the center O of the circumcircle
Regular polygon conversion formula table
|
each amount |
equilateral triangle |
square |
regular pentagon |
hexagon |
regular n -gon |
|
picture shape Sa Rr |
|
|
|
Ra
|
|
Regular polygon scale coefficient table
|
n |
|
|
|
a/R |
R/a |
r/a |
|
3 4 5 6 7 8 9 10 12 15 16 20 |
0.4330 1.0000 1.7205 2.5981 3.6339 4.8284 6.1818 7.6942 11.196 17.642 20.109 31.569 |
1.2990 2.0000 2.3776 2.5981 2.7364 2.8284 2.8925 2.9389 3.0000 3.0505 3.0615 3.0902 |
5.1962 4.0000 3.6327 3.4641 3.3710 3.3137 3.2757 3.2492 3.2154 3.1883 3.1826 3.1677 |
1.7321 1.4142 1.1756 1.0000 0.8678 0.7654 0.6840 0.6180 0.5176 0.4158 0.3902 0.3129 |
0.5774 0.7071 0.8507 1.0000 1.1524 1.3066 1.4619 1.6180 1.9319 2.4049 2.5629 3.1962 |
0.2887 0.5000 0.6882 0.8660 1.0383 1.2071 1.3737 1.5388 1.8660 2.5323 2.5137 3.1569 |
|
n |
|
|
|
a/R |
R/a |
r/a |
|
twenty four 32 48 64 |
45.575 81.225 183.08 325.69 |
3.1058 3.1214 3.1326 3.1366 |
3.1597 3.1517 3.1461 3.1441 |
0.2611 0.1960 0.1308 0.0981 |
3.8306 5.1012 7.6449 10.190 |
3.7979 5.0766 7.6285 10.178 |