§ 5 Polynomials
[ Integer-valued polynomial ] When the variable x is an integer , the value of a polynomial f ( x ) is always an integer, and this polynomial is called an integer-valued polynomial.
Integer-coefficient polynomials are a special case of integer-valued polynomials.
Integer-valued polynomial expressions:
1 ° where the nth integer polynomial can be expressed as
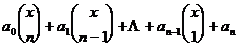
where is an integer,![]()
![]()
2 ° integer-valued odd polynomial ( satisfying f ( - x ) = - f ( x )) must be expressed as
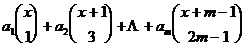
where is an integer .![]()
A 3 ° integer-valued even polynomial ( satisfying f ( - x ) = f ( x )) must be expressed as
![]()
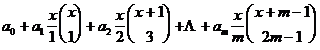
where is an integer .![]()
[ Reducible and irreducible polynomials ] Let f ( x ) be a polynomial with rational coefficients , if there are non-constant polynomials with rational coefficients g ( x ) and h ( x ), such that
f ( x ) = g ( x ) h ( x )
Then f ( x ) is called reducible ( or reducible) in the field of rational numbers , otherwise f ( x ) is called an irreducible polynomial over the field of rational numbers ( abbreviated as irreducible polynomial ).
[ Gauss's theorem ] Let f ( x ) be an integer coefficient polynomial , which is reducible in the rational number field , then there must be two integer coefficient polynomials g ( x ) and h ( x ), such that
f ( x ) = g ( x ) h ( x )
[ Eisenstein's test ]
1 ° is set as . If there is a prime number p , such that ![]()
![]() but
but ![]()
Then f ( x ) is an irreducible polynomial .
2 ° is set as a polynomial of degree 2n+ 1 integer coefficient , if there is a prime number p , such that ![]()
![]()
but ![]()
Then f ( x ) is an irreducible polynomial .
[ Pylon's Discrimination Method ]
1 ° set
![]()
is an integer coefficient polynomial of degree n with a coefficient of 1 , which satisfies the conditions :
(i)
![]()
(ii)
![]()
(iii) ![]() Real numbers )
Real numbers )
Then f ( x ) is an irreducible polynomial .
2 ° set
![]()
is an integer coefficient polynomial of degree n with a coefficient of 1 , which satisfies the conditions :
(i)
![]()
(ii) ![]()
Then f ( x ) is an irreducible polynomial .
3 ° set
![]()
is an integer coefficient polynomial of degree n with a coefficient of 1 , which satisfies the conditions :
![]()
Then f ( x ) is an irreducible polynomial .
4 ° set
![]()
is an integer coefficient polynomial of degree n with a coefficient of 1 , which satisfies the conditions :
![]()
![]()
Then f ( x ) is an irreducible polynomial .
5 ° set
![]()
is an integer coefficient polynomial of degree n whose first term is 1 and whose constant term is not zero , and satisfies the conditions :
![]()
Then f ( x ) is an irreducible polynomial .
[ Divisibility of Polynomials ] Let f ( x ) and g ( x ) be polynomials with two rational coefficients , and g ( x ) is not always zero , if there is a polynomial h ( x ) such that
f ( x ) = g ( x ) h ( x )
Then g ( x ) is said to be divisible by f ( x ), denoted as
![]() or
or ![]()
At this time , g ( x ) is called a factor of f ( x ) , and f ( x ) is called a multiple of g ( x ) . Otherwise , g ( x ) cannot divide f ( x ), which is written as .![]()
The following ¶ ° f represents the degree of the polynomial f ( x ) .
The divisibility of polynomials has the following properties :
1 ° ![]()
2 ° If and , then f and g differ only by a constant factor . ![]()
![]()
3 ° If , then ![]()
![]()
![]()
4 ° if , then¶ ° f ¶ ° g _ ![]()
![]()
If , and , then f is called a true factor of g , obviously ¶ ° f < ¶ ° g.![]()
![]()
5 ° If p ( x ) is an irreducible polynomial , and , then or . ![]()
![]()
![]()
6 ° If p ( x ) is an irreducible polynomial , and
f ( x ) = 0, p ( x ) = 0
If there is a common root , there must be .![]()
[ Polynomial with remainder division ] Let f ( x ) and g ( x ) be arbitrary polynomials , and g ( x ) is not always zero , then there must be two polynomials q ( x ) and r ( x ) such that
f ( x ) = g ( x ) q ( x ) +r ( x )
where r ( x ) = 0 or ¶ ° r< ¶ ° g. This is called polynomial division with remainder .
[ Polynomial rolling division method ] The definition of polynomial rolling and rolling division method and integer rolling division method are completely similar , and it is only necessary to regard the literal symbols in the formula in § 1(1) of this chapter as polynomials .
Similarly , the unique decomposition theorem of polynomials , the highest common factor and the lowest common multiple, and the concepts and formulas of polynomial coprime are completely similar to those in the section on integers , and it is only necessary to regard the symbols in the corresponding formulas as polynomials .
Example Polynomial
![]() and
and![]()
The highest common factor of .
Solution To avoid fractions , multiply f ( x ) by 2 , then divide f ( x ) by g ( x ) :
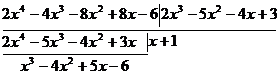
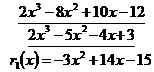
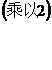
During the calculation , the first difference is multiplied by 2 , so the quotient is changed , but the remainder only obtains a number factor of 2, which does not matter . Multiply g ( x ) by 3 , and divide by :![]()
![]()
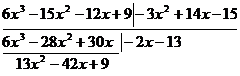
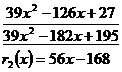
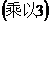
desirable![]()
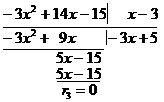
So the required common factor is .![]()
[ Congruence ]
1 ° polynomial mode congruence Let m ( x ) be a polynomial , if
![]()
Then f ( x ) and g ( x ) are said to be congruent modulo m ( x ) , denoted as
![]()
2 ° Prime Modulo Congruence Let p be a prime number , f ( x ) and g ( x ) are polynomials with integer coefficients , if the corresponding coefficients are all congruent modulo p , then the two polynomials are said to be congruent modulo p , and write do
![]()
3 ° Multiple modular congruence formula Let p be a prime number , ( x ) is a polynomial , if f ( x ) - g ( x ) is a multiple of ( x ) , mod p , then f ( x ) and g ( x ) Congruence modulo p, ( x ) , denoted as ![]()
![]()
![]()
f ( x ) g ( x )![]()
![]()
[ Promotion of Fermat's Theorem ] Let p be a prime number , ( x ) ![]() is an irreducible polynomial of degree n , mod p, then for any polynomial that is not a multiple of ( x ) f ( x ), mod p, there is always
is an irreducible polynomial of degree n , mod p, then for any polynomial that is not a multiple of ( x ) f ( x ), mod p, there is always![]()
![]()
![]() 1
1![]()
For any polynomial there is always
![]()
![]() f ( x )
f ( x )
![]()
very
![]()
![]() x
x ![]()