§ 6 Algebraic Numbers
[ Algebraic Numbers ] If q is an algebraic equation whose coefficients are rational numbers
The root of , then q is called an algebraic number . After general division , q satisfies an algebraic equation with rounded coefficients , so an algebraic number can also be defined as "the root of an algebraic equation with rounded coefficients ".
If f ( x ) is an irreducible polynomial in the field of rational numbers , and , then q is called an algebraic number of degree n . Obviously , an algebraic number of first degree is a rational number .
Algebraic numbers have the following properties :
1 ° The sum, difference, product, and quotient of two algebraic numbers ( with non-zero division ) are still algebraic numbers .
The roots of algebraic equations whose coefficients are algebraic numbers are still algebraic numbers .
[ Algebraic Integer ] If q is the root of an n -th degree irreducible algebraic equation in which one coefficient is 1 and the other coefficients are rational integers , then q is called an n -th degree algebraic integer .
Algebraic integers have the following properties :
If the 1 ° algebraic integer is a rational number ( that is, a first-order algebraic integer ), it must be a rational integer .
2 ° The sum, difference and product of two algebraic integers are still algebraic integers .
3 ° The first coefficient is 1, and the roots of the algebraic equations whose other coefficients are algebraic integers are still algebraic integers .
4 ° If q is an algebraic number , it satisfies the rational integer coefficient equation
is an algebraic integer .
5 ° If q is an algebraic integer of degree n , then the power of q can be expressed as 
where i is a non-negative integer , all of which are rational integers .
6 ° If q is an algebraic number of degree n , then the power of q satisfies the equation 
where i is a non-negative integer , which is a rational integer .
[ Unit number ] If both q and q are algebraic integers , then q is called a unit number .
Unit numbers have the following properties :
The necessary and sufficient conditions for 1 ° q to be a unit number are : q is the root of the rational integer coefficient algebraic equation whose leading term is 1 and the constant term is 1 . 
2 ° The leading coefficient and constant term are all unit numbers , and the roots of algebraic equations whose other coefficients are algebraic integers are unit numbers .
[ algebraic extension ]
1 ° Single extension field , let q be an n -th algebraic number , then the form is
( Coefficients are rational numbers )
The totality of the numbers constitutes a field . It is called the n -time single extension field obtained by adding q to the rational number field Q , denoted as Q ( q ). If , then Q ( q ) is the addition, subtraction, and multiplication of the algebraic number q . , the largest set of numbers produced by division ( divisor non-zero ) .
2 ° Finite extended field The field generated by the addition, subtraction, multiplication and division of a finite number of algebraic numbers ( the divisor is not zero ) is called the finite extended field on Q , denoted as 
K = Q ( )
A finite extension field must be a single extension field , that is, there is an algebraic number q such that
Q ( ) = Q ( q )
The degree of q is called the degreeof the finite extended field Q ().
[ Conjugate number ] Let q be an algebraic number of degree n , and q satisfies an irreducible polynomial of degree n on the rational number field
Note , and set the other n - 1 roots of the polynomial , then it is called the conjugate root of q .
Any algebraic number a Q ( q ), then a can be uniquely represented as
(1)
where is a rational number . Remember , then
is called the conjugate number of a .
[ Trace and Moment of Algebraic Numbers ] Let a K = Q ( q ), note , let it be the conjugate number of a , then respectively call
is the trace and moment of the algebraic number a , which is defined as formula (1) .
Note that the trace and moment here are for the field K , and the moment is also called the norm . Another definition of them is: Let the minimal polynomial of a ( the lowest degree irreducible multinomial with a as the root ) be
order , then
Traces and moments have the following properties :
1 ° If a is an algebraic number , then the trace and moment of a are rational numbers .
2 ° If a is an algebraic integer , then the trace and moment of a are rational integers . If a is a non-zero algebraic integer , then . 
The necessary and sufficient conditions for the 3 ° algebraic integer a to be a unit number are : . 
4 ° S ( a + b ) = S ( a ) + S ( b )
N ( a b ) = N ( a ) N ( b )
[ Basics and whole bases of algebraic number fields ]
1 ° basis Let K be an n -th algebraic extension field , which is a set of algebraic numbers in K. If any algebraic number g in K can be uniquely represented as 
is a rational number in the formula , then it is called a set of basis of K. Obviously , it is linearly independent in the rational number field .
The necessary and sufficient conditions for being a set of bases of domain K are :
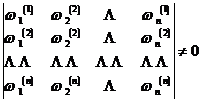
where is the conjugate number , j= .
If K=Q ( q ), then it is a set of basis of K.
2 ° Integer base Let K be an n -th algebraic extension field , a set of algebraic integers in K , if any algebraic integer g in K can be uniquely represented as
where is a rational integer , it is called a set of integral bases of K.
If a group uses
is the smallest algebraic integer , then this set is a set of integral bases .
[ Quadratic field ] Let D be a rational integer without square factor . Then Q ( ) 
is a quadratic field . Any algebraic number in Q ( ) can be expressed as
where a and b are both rational numbers .
Let D be a rational integer with no square factor .
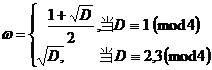
Then 1, w are a set of integral bases of the quadratic field Q ( ) .
In general , the n -th field Q may not necessarily be able to find the algebraic integer w , so that
a set of integral bases that form Q ( q ) .
[ Gaussian field ] Let Q ( i ) be called the Gaussian field , which is a quadratic field .
Any number in the Gaussian domain can be expressed as
In the formula, a and b are both rational numbers . When both a and b are rational integers , a+bi is called a Gaussian integer .
The Gaussian field has four unit numbers : , 
all of which have moments of 1.
[ Cycloidal field ] Let m be a positive integer , and the field S formed by adding all the roots of the polynomial to Q is called the m -th degree unit root on Q.
There is anm-order primitive unit root q in S ( q isa root,but nota root(n<m), and q iscalledm-order primitive unit root),so thatS = Q( q ),and the A set of bottoms.
If q is an m -th primitive unit root , so that it is also an m -th primitive unit root , there are ( m ) in total , where ( m ) is the Euler function .
[ decomposition theorem ]
1 ° Divisibility If a and b are two algebraic integers , when they are still algebraic integers , then b is said to be divisible by a , denoted as . At this time, a is said to be a multiple of b , and b is a factor of a . 
2 ° Associativity If two algebraic integers a and b differ only by a single factor , then a and b are said to be associative .
Obviously : (i) a combines with a ; (ii) if a combines with b , then b combines with a ; (iii) if a combines with b , and b combines with g , then a and g combine Combine .
3 ° Indecomposable If the algebraic integer a in K has two other algebraic integers b, gK , and neither of them is a single number , such that
a = b g
Then a is said to be decomposable in the field K , otherwise it is said to be non-decomposable .
4 ° Decomposition Theorem Any algebraic integer in K can be decomposed into the product of non-decomposable algebraic integers .
If this decomposition is unique regardless of order and associativity , it is called unique decomposition .
The unique decomposition theorem of the Gaussian field holds .
The unique decomposition theorem in the quadratic domain holds , it is now known that there are
Q ( ), D = 2, 3, 5, 6, 7, 13, 17, 21, 29 , etc.
Not all unique factorization theorems of quadratic fields hold , for example , the unique factorization theorem of Q ( ) 
does not hold :
