§ 4 Scale space and consistent space  

 

1.     Scale space

 

    [ Scale, distance and scale space ] Assuming that D is a set and j is a transformation that transforms D ′ D into R ¹ , if for all x D , y D , z D , the condition is satisfied:  

    (i) j  ( x , y ) 3 0 , the equal sign is only true when x = y , where j ( x , y ) = j ( < x , y > );

    (ii) j  ( x , y ) = j ( y , x );

    (iii) j  ( x , y ) + j ( y , z ) 3 j ( x , z ) .

Then call j a scale of D , j ( x , y ) is the distance between x and y at the scale of j , and D is the scale space (distance space) with j as the scale .

    If the condition ( i ) does not add "the equal sign is only true when x = y ", and the rest ( ii ) and ( iii ) are the same, then j is called a quasi-scale of D.

    [ Topology of Scale Spaces ] Assuming that j is a scale of the set D , for a point a D and a real number r , call { x | j ( x , a ) < r } (when r 0 it represents the empty set) as a is a sphere whose center r is a radius . The topology propagated by all the spheres is called the scale topology of D. In fact, the whole of all the spheres is a basis of this topology . If there is no other statement in the future, the scale space All assume a topological space with this scale topology as the topology . 

    Assuming that a is a point in the scale space, then the totality of all the spheres with a as the center and rational numbers as the radius is a neighborhood basis of a . Therefore, the scale space must be the first countable space . In addition, it is not difficult to see , the scale space must be T2 _space .

    [ Scaling and Scaling Theorem ] Assuming that the bearing point set of a topological space X has a scale, and the topology obtained from this scale is equal to the original topology of X , then X is said to be scalable . 

    Suppose Φ is the totality of a family of point sets in a topological space X. If every point in X has a neighborhood with at most a finite number of points belonging to Φ in common, then Φ is said to be locally finite; especially if any two Each packet belonging to the point set of Φ has no common point, then Φ is said to be insulating .

    Theorem The necessary and sufficient conditions for a topological space X to be scalable are: X is a T ₃ space and the topology of X has a basis that is the sum set of countable locally finite families (here "local finite" can be changed to "insulation", T ₃ It can also be changed to T ₄ ) . 

    [ n -dimensional Euclidean space and Cartesian coordinate method ] Assume that X is a scale space with j as the scale, and assume that there ^is a one-to -one transformation f that transforms X into an n -dimensional real number space Rn , so that for any two in X points x and y , 

                     

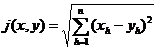
established , here , then X is called n -dimensional Euclidean space, referred to as n -dimensional Euclidean space, denoted as En ^, f is a Cartesian coordinate method of En , called the Cartesian coordinate of point ^x , called this right angle The origin in the coordinate method .

    ^{The Cartesian coordinate method of En} exists but is not unique . Assuming that f and E ⁿ are the Cartesian coordinate method of En, f ' ( O _f ) =< b ₁ , × × × , b _n > , and any point x in En ^is at The coordinates under f and f' are denoted as < x ₁ , × × × , x _n > and < x ₁ ', × × × , x respectively_n ' >, then since

                       

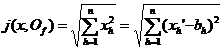
get

Here ( a _hk ) is an n ′ n orthogonal matrix .

    Conversely, as long as ( a _hk ) is any n ′ n orthogonal matrix , b ₁ , × × × , b _n is any n real numbers, then the above set of equations represents a new Cartesian coordinate method . So the right angle There are infinitely many coordinate methods, and the transformation between different Cartesian coordinate methods is the combination of the so-called "rotation axis" and "shift axis" .

    In addition, a Cartesian coordinate method f of ^En is actually a topological transformation that transforms En onto R n, so the image of ^a tee in En under f is the ^sum set of a family of ⁿ - dimensional intervals in R ⁿ , in turn, the image source of an n -dimensional interval in R ^{n is the sum} set of kick-offs in En .

    Therefore , a scale can be set in R ⁿ to make it E ⁿ . This also proves the existence of n -dimensional Euclidean space .

    [ Completion of the space ] Assume that X is a scale space with j as the scale . If < x _n | n ω > is a point sequence in X , for any positive number e , there is always a positive integer N such that 

                               j ( x _n , x _m ) < e

Comparing all positive integers n and m larger than N hold, then < x _n | n ω > is called the Cauchy column in X.

    Any convergent point sequence in a scale space must be a Cauchy sequence, but a Cauchy sequence is not necessarily convergent . For example, if all rational numbers S are regarded as subspaces of the one-dimensional real number space R ¹ , then the Couchy sequence in S Ciel may not converge (because its limit may be irrational) .

    If any Cauchy column in a scale space X converges, then X is said to be complete .

    Assuming that both X and X ' are scale spaces, X' is complete, and there is a transformation f that transforms X into X' isomorphically , and the image f ( X ) of X is dense everywhere in X' , then we say X' is the completion of X.

    Theorem Any scale space has a completeness, and any two completenesses are equal-scale homeomorphism . 

    As long as one Cauchy column in the scale space is regarded as an element, and the distance between two Cauchy columns is properly specified (when the distance is equal to zero, the two elements are considered to be the same), it is not difficult to prove that all these elements are a complete set .

    Considering the absolute value of the difference between two real numbers as the distance between the two real numbers, then the one-dimensional real number space R ¹ is the completeness of all rational numbers . This method can be used to establish the concept of irrational numbers .

    Of course, the Cauchy column can be generalized into a Cauchy net . However, since the scale space satisfies the first countable axiom, the same completeness can only be obtained with the concept of a Cauchy net .

    [ Consistently convergent topology of a family of bounded transformations ] Assuming that A is a set and Y is a scale space, the set of all bounded transformations that transform A into Y (transformation that transforms A into a tee is called bounded transformations) Let it be denoted as F. The distance specified in F is as follows: Let f F , g F , then their distance 

                       J ( f , g ) = j ( f ( x ), g ( x ))

Here j represents the scale in Y. The scale topology of F produced by J is called the uniformly convergent topology of F.

    Note that the uniformly convergent topology of F is defined only by the scale of Y , and does not involve the topology of A.

    Compared with other topologies, the uniform convergence topology of the theorem bounded transformation family F is characterized by: under this topology, the sufficient and necessary conditions for the convergence of any point net < f _p | p Q > in F are: for all x A , < f _p ( x )| p Q > uniformly converges in A (that is, for any positive number e , there exists a q Q , for all x A and all p>q in Q ,

                             j ( f _p ( x ) , f _q ( x ) ) < e

established) .

    F can be regarded as a subset of A ^Y. Therefore , the point-to-point convergence topology of A Y has an induced topology in ^F , which may be called the point-to-point convergence topology of F , because it is also converged by "point- to -point convergence" . The topology is thinner than the point-to-point convergent topology . Because under uniformly convergent topology, for every point f F , all sets { g | for all x A , j ( g ( x ), f ( x ) ) < e } ( e is an arbitrary positive number) constitutes a neighborhood basis . Under the point-to-point convergence topology, for each f F , all sets { g | There are finite x A such that j ( g ( x ) , f ( x ) ) < e } constitutes a neighborhood basis . Each set of the latter neighborhood basis obviously masks a set of the former neighborhood basis, But not the other way around .

 

2.     Consistent space

 

    [ Composite relation and inverse relation ] Assuming that X is a set, and u and are two relations in X (that is, u X ′ X , v X ′ X ) , it is specified that 

                     u ={< x , y > | x X , y X , and there exists z X such that

< x , z > u and < z , y > }

u is of course also a relation in X , called the compound relation of u and .

    re-specify

u ^-1 = {< x , y > | < y , x > u } ,

Then u ^-1 is also a relation in X , called the inverse relation of u .

    easy to prove

( u ) ^-1 = V ^-1 u ^-1

    [ Consistent space ] Assume that X is a set, U is a non-empty relational family in X (i.e. U 1 φ and U í ^{X ′ X} 2 ), and satisfy the conditions: 

    (i) If u U , then for any x X , < x , x > u ; 

    (ii) if u U , then there is U , so that u ;

    (iii) If u U , then u ∩ U ;

    (iv) If u U , u X ′ X , then U ;

    (v) If u U , then u ^-1 U .

    Then U is called a uniformity of X , and < X , U > is called a uniform space (sometimes X is called a uniform space under the uniformity of U ) .

    The U that satisfies the conditions ( i )—( iv ) is called a quasi-consistency of X , and the corresponding < X , U > is called a quasi-consistent space .

    If U and U' are two congruences of set X , U U' , then U is said to be thicker than U' and U ' thinner than U.

    Assuming that there is a non-empty relation family V in the set X that satisfies the conditions ( i ) and ( ii ) of the definition, then all the general sets U _{0 of} X that cover the consistency of V are also a consistency, which can cover V The crudest identity is called the identity reproduced by V, and V is called a subunit of U ₀ * . Assuming that V is a subunit of identity U ₀ , and for any u U ₀ there is V such that u , then it is called V is a basis _of U0 .

    For any set X , the consistency propagated by {{< x , x >| x X }} is the finest consistency .

    The scale space can be regarded as a special case of the consensus space: assuming that X is a scale space, the relationship family in X {{< x , y >| The distance between x and y is less than γ }| γ is a positive number } breeds the consensus The property is called the consistency produced by the scale of X. Usually , unless otherwise stated, a scale space X is always regarded as a consistent space under this consistency . In fact, the above condition of " γ is a positive number" can be changed to " γ is a positive rational number" (due to the condition ( iv ) of consistency), so the consistency produced by the scale must have a countable basis .

    [ Scaling of uniform topology and uniform space ] Assume that < X , U > is a uniform space . For x X , u U , let { y |< x , y > u } be denoted as u [ x ] , called x ’s A neighborhood . The topology propagated by all such neighborhoods is called the consistent topology of X. A consistent space X is always regarded as a topological space under a consistent topology unless otherwise stated . 

    If a scale can be specified in a uniform space, and the uniformity produced by this scale is the same as the original uniformity, then the uniform space is said to be scalable .

    A necessary and sufficient condition for a consistent space to be scalable is that its consistency has a countable basis, and it is a T2 space . _A necessary and sufficient condition for a consistent space to be quasi-scalable is that its consistency has a countable basis base .

    [ Consistent Continuity and Consistent Isomorphic Transformations ] Assuming that < X , U > and < Y , V > are two consistent spaces, f is a transformation that transforms X into Y , if for any V , there is always u U , so that All < x , y > u , < f ( x ) , f ( y ) > are established, then f is called uniformly continuous . Uniform continuity must be continuous, but continuity may not be uniformly continuous under uniform topology . 

    A reversible uniform continuous transformation on a variable is called a uniform isomorphic transformation . A uniform isomorphic transformation must be a homeomorphic transformation, but the converse is not necessarily true .

    [ Consistent convergence ] Assume < Y , V > is a consistent space, X is a set, and < f _p | p Q > is a point net in X Y, ^f X Y ^, if for any V there is a q Q is such that for all p > q and all x X , 

                       < f _p ( x ), f ( x ) > V

is established, then < f _p | p Q > is said to converge to f uniformly .

    Assuming that < Y , V > is a consistent space and X is a set, then a consistent convergent consistency can also be specified for ^X Y as follows: For any V , a relation w in ^X Y can be obtained

               w = {< f , g >| holds for all x ^X X , < f ( x ), g ( x ) > } .

The consensus propagated by the totality of all these ws is called the uniformly convergent consensus of X ^Y. The topology produced by this consensus is called the consensus convergent topology of ^X Y. It can be seen that a point net in ^X Y is consistent Convergence means converging under a uniformly convergent topology .