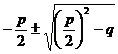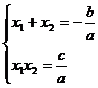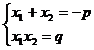Chapter 3 Algebraic Equations

 

The theory of algebraic equations has the following main problems:

   (1) Radical solution to the problem;

          (2) Root distribution and approximate calculation;

          (3) There is a problem with the root;

(4) Research on the properties of roots .

This chapter focuses on the introduction of ( 1 ) and ( 2 ), and only briefly describes the two problems ( 3 ) and ( 4 ) .

The problem of radical solution is how to formulate the roots of the equations. Here, the expressions of the roots of the second, third and fourth degree equations in the real number field are listed in detail, and the relationship between the roots and the coefficients is pointed out, and Abbe is also described. Ear's Theorem, that algebraic equations of the fifth degree and higher have no general solutions to radicals . This chapter introduces the properties of algebraic equations, mentions the important "fundamental theorem of algebra" about the existence of roots; and describes Galois It is pointed out that there are specific equations that cannot be solved by algebraic methods; some special solutions of algebraic equations and the fundamental theorems of symmetric polynomials are also introduced; various discrimination methods for the isolation of roots are given . Finally, the real roots of equations are introduced. A variety of methods for approximate calculation, and the Qin Jiushao method is explained in detail .

 

§ 1   Expressions for the roots of second, third, and fourth degree equations

 

1. Basic Concepts

[ Number field ]   A number system is called a number field if it satisfies the following two conditions:

(i) There are numbers not equal to zero in the series;

(ii) The sum, difference, product, and quotient of any two numbers in the system (these two numbers can also be the same) (zero cannot be used as a divisor) are still the numbers in the system. Operations are closed .

       For example, rational, real, and complex coefficients are all number fields .

       [ roots of a polynomial ] have the   form

f ( x )= a ₀ x ⁿ + a ₁ x ^{n -1} + a ₂ x ^{n -2} + L + a _{n -1} x + a _n =0

The equation of is called an n -degree algebraic equation of an unknown on a number field S , f ( x ) is called a univariate n -degree polynomial, where n is a positive integer, a ₀ , a ₁ , a ₂ , L , a _{n -1} , a _n is a constant belonging to the number field S , which is called the coefficient of the equation, and the highest-order coefficient a ₀ is abbreviated as the leading coefficient .

       Let c be a constant so that f ( c )=0, then c is called the polynomial f ( x ) or the root of the equation f ( x )=0 . In this section, the second, third and fourth degree equations in the real number field are considered first . .

      2. Quadratic equation

Expressions of the roots of quadratic equations and the relationship between roots and coefficients

equation	ax 2 + bx + c = 0	x 2 + px + q = 0
root expression	x 1,2 =	x 1,2 =
Relationship between roots and coefficients
Discriminant	= b 2 - 4 ac >0 has two unequal real roots =0 has two equal real roots <0 has two complex roots	= p 2 - 4 q >0 has two unequal real roots =0 has two equal real roots <0 has two complex roots

       3. Cubic equation

       [ x ³ - 1=0]   Equation x ³ - 1=0                  

The three roots of are x ₁ =1, x ₂ = ω = , x ₃ = ω ² = ( i ² = - 1) (1)             

       [ x ³ + px + q = 0 ( Cardan formula )]    equation

x3 + px + q ⁼ 0

The three roots of

           x1 ₌ _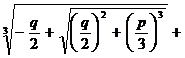   

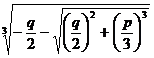
           x ₂ = ω ω ² ₍₂₎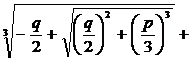     

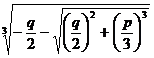
           x ₃ = ω ² ω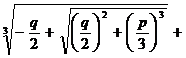

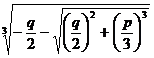
where ω , ω ² are the same as (1). This is called Cardan's formula .

       The relationship between the root and the coefficient is

x ₁ + x ₂ + x ₃ =0, , x ₁ x ₂ x ₃ =      - q

       The discriminant is

=

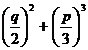
When >0 , there is one real root and two complex roots; when =0 , there are three real roots, and when p = q =0 , there is one triple zero root; at that time , two of the three real roots are equal; When < 0 , there are three unequal real roots .

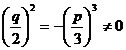
       The trigonometric function expression for the three roots (only when p < 0 ) is

                          x ₁ =2 cos θ

                          x ₂ =2 cos( θ +120°)

                          x ₃ =2 cos( θ +240°)

in the formula

r = , θ = arc cos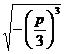   

       [ ax ³ + bx ² + cx + d =0]   General cubic equation

ax ³ + bx ² + cx + d = 0       

Divide the above formula by a and set

x = y

is transformed into the following form

y ³ + py + q = 0

According to the situation of ( 2 ), y ₁ , y ₂ , y _{3 can be solved} , then the three roots of the general cubic equation are

x ₁ = y ₁ , x ₂ = y ₂ , x ₃ = y ₃  

The relationship between the three roots and the coefficient is

x ₁ + x ₂ + x ₃ = , , x ₁ x ₂ x ₃ =    

       4. Quadratic equation

       [ ax ⁴ + cx ² + e = 0]   equation

ax ⁴ + cx ² + e = 0

, set y = x ² , then it becomes a quadratic equation

ay ² + cy + e = 0

The four roots can be solved as

                                   x _1,2,3,4 =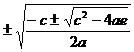

[ ax ⁴ + bx ³ + cx ² + bx + a =0]   equation

ax ⁴ + bx ³ + cx ² + bx + a = 0

, set y = x + , then it becomes a quadratic equation, and the four roots can be solved as

x _1,2,3,4 = , y = 

[ x ⁴ + bx ³ + cx ² + dx + e =0]        general quartic equation

ax ⁴ + bx ³ + cx ² + dx + e = 0

can be reduced to a quartic equation with a leading coefficient of 1 , and the equation

x ⁴ + bx ³ + cx ² + dx + e = 0

The four roots of are exactly the same as the four roots of the following two equations:

x ² + ( b + ) ( y + ) = 0

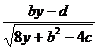
x ² + ( b - ) ( y - ) =0

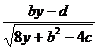
where y is the cubic equation

8 y ³ -4 cy ² +(2 bd -8 e ) y + e (4 c - b ² ) - d ² =0

any real root of .

       5 . Abel's theorem

       There is no general algebraic solution for algebraic equations of the fifth degree and higher (that is, the method of finding the roots from the coefficients of the equation through finite-order arithmetic and square rooting) . This is Abel's theorem .