§ 3 Special solutions to algebraic equations
Abel proved that there are no algebraic solutions to general equations of degree 5 and higher . But Abel's theorem does not answer the question: is there an algebraic solution to each given specific equation . Galois proved that there is an algebraic solution A specific integer-coefficient algebraic equation that cannot be solved by the method . For example
x 5 - x +1=0
Galois also found necessary and sufficient conditions for equations to be solved by radicals .
1. Find rational roots
According to the properties of "whole roots and rational roots" in the previous section, the rational roots of some specific equations can be found .
Find the rational roots of an equation . 
Solution Since p and q of the rational roots of this equation are both divisors of 2 , they are 1 , -1 , 2 , and -2 . So the possible values are 1 , -1 , 2 , and -2 . Divide by synthesis ( See § 2 , a ) 
test:
1) 2 - 3 2 2 - 1) 2 - 3 2 2
2-1 1-2 5-7 _ _ _ _ _ _
2 - 1 1 3
2 - 5
7 - 5
2 - 3 2 2 2
- 3
2 2
1 - 1 
- 1
2 - 2
2 - 2 1 2 
- 4
4 0
So it is a rational root of the known equation .
Divide the original formula by , get the quotient formula
which is 
The tower top discriminant 4 - 8<0 , its two roots are a pair of conjugate complex roots . Therefore, the original equation has only one rational root .
2. Solve three equations
Shaped like
au 2 n + bu n +c =0
The equation of is called a three-term equation, where a, b, c, n are not equal to zero , n is an integer . It can be solved by radicals . Let u n = x , the quadratic equation ax 2 + bx+c =0.
Solve the equation by example
Solve the order , then get , its root is and . From get . So. Substitute into the original equation to check, we can see that these four numbers are the roots of the equation . 
3. Solve the reciprocal equation
Shaped like
ax n + bx n − 1 + cx n − 2 + L + cx 2 + bx + a =0
(where the coefficients of the xn -k and xk terms are the same) is called the reciprocal equation . Any root of the reciprocal equation is not equal to zero .
Divide both sides of the 1° even-numbered ( n = 2 k ) reciprocal equation by x k , and then set z = x + , the original equation can be transformed into a k -th equation of z , solve this equation, get the value of z , and then the corresponding x The value can be determined by the quadratic equation
x 2 - zx +1=0
ask for.
2° Solution of odd-numbered ( n = 2 k +1) reciprocal equations boils down to solving even-ordered reciprocal equations .
Solve the equation by example
The solution is a root of the original equation, and the equation is divided by the 4th reciprocal equation: 
Divide it by , and then combine, we get
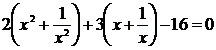
Let , then , the above formula becomes
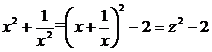
From this, there are two definite equations:
and 
From this we get
4. Solve the binomial equation
In the form of x n - A =0
The equation of is called a binomial equation . Its n roots are the nth roots of the complex number A.
If A is written as
A = r ( cos θ + i sin θ )
Then the n roots of the equation x n - A = 0 are
( k = 0 , 1, 2 , L , n - 1)
Geometric Explanation: The points on the complex plane that correspond to the nth root of the number r ( cos θ + i sin θ ) are the vertices of a regular n - gon , and these vertices are on a circle with the origin as the center and the radius . And One of the vertices of this n -gon has an argument . Figure 3.1 shows the case of n = 6 .
If A =1 , then the solution ξ of x n =1 is called n -th unit root . The n n - th unit roots are
cos + i sin ( k = 0,1,2, L , n - 1) Figure 3.1
If ξ is one of the n -th unit roots, then the n n - th unit roots are 1, ξ , ξ 2 , L , ξ n - 1 , which are geometrically represented as vertices of an inscribed regular n -gon of the unit circle .
