Chapter 4
Matrices , Determinants , Linear Equations
This chapter includes two parts: matrices , determinants, and systems of linear algebraic equations .
In the previous part, the basic concepts of matrices and determinants were described, with emphasis on the properties and basic operations of various types of matrices. In addition, the methods for finding eigenvalues and eigenvectors of matrices were also introduced, as well as related content, such as similarity transformation, etc. ;In the part of linear equations, it focuses on the solution of n equations with n unknowns , and also briefly discusses the structure of the solution . Finally, it also briefly explains the integer coefficient linear equations and linear inequalities .
§1 Matrix and determinant
1. Matrix and its rank
[ Matrix and Square Matrix ] Number field (Chapter 3, § 1 ) The m × n numbers a ij ( i =1,2, … , m ; j =1,2, … , n ) on F are determined by A rectangular array of positions, called an m × n matrix . Denoted as
A =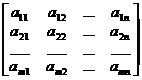
The horizontal row is called the row, the vertical row is called the column, a ij is called the element of the i -th row and the j -th column of the matrix, and the matrix A is abbreviated as ( a ij ) or ( a ij ) m ′ n .
An n - by - n matrix is also calledsquare matrix of order n , and a 11 , a 12 , ..., a nn are called the elements ofthe main diagonal ofmatrix A.
A matrix whose number of rows m and number of columns are both finite is called a finite matrix . Otherwise, it is called an infinite matrix .
[ Linear correlation of vectors is linearly independent ] For a set of vectors x 1 , x 2 ,..., x m in n -dimensional space , if there is a set of numbers k i ( i = 1 , 2 ,... , m ) , so that
k 1 x 1 + k 2 x 2 + … + k m x m =0
If established, the set of vectors is said to be linearly dependent on F , otherwise the set of vectors is said to be linearly independent on F.
Discussion of Linear Dependency of Vector Groups:
A sufficient and necessary condition for the linear correlation of 1 ° vector groups x 1 , x 2 , ..., x m is that at least one vector x i can be represented by a linear combination of other vectors, that is
2 ° The set of vectors containing zero vectors must be linearly dependent .
In the 3 ° vector group x 1 , x 2 ,..., x m , if two vectors are equal: x i = x j ( i ≠ j ), then the vector group is linearly related .
4 ° If the vector groups x 1 , x 2 ,..., x r are linearly correlated, the vector group formed by adding several vectors is still linearly correlated; if the vector groups x 1 , x 2 ,..., x m are linearly independent, Then the vector group composed of any part of the vector is also linearly independent .
5 ° If x 1 , x 2 , . _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ a linear combination of .
[ Row Vector and Column Vector · Matrix Rank ] An n -dimensional vector composed of elements in any row of the matrix is called a row vector , and is written as
a i =( a i 1 , a i 2 ,..., a in ) ( i =1,2,..., m )
The m -dimensional vector formed by the elements of any column of the matrix is called a column vector, denoted as
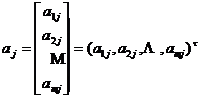( j =1 ,2 ,..., n )
In the formula, t represents transposition, that is, the row (column) is converted into a column (row) .
If r of the n column vectors of matrix A are linearly independent ( r ≤ n ) , and all column vector groups whose number is greater than r are linearly correlated, then the number r is called the column rank of matrix A. Similarly, matrix A can be defined row rank .
The column rank and row rank of a matrix A must be equal, it is also called the rank of the matrix, denoted as rank A = r .
The rank of a matrix is also equal to the maximum order of subforms (see this section, two) in that matrix that are not equal to zero .
Second, the determinant
1. The determinant and its Laplace expansion theorem
[ Nth order determinant ] Let
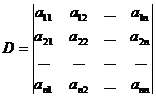
is a number determined by n 2 numbers a ij ( i , j =1,2,..., n ) arranged in the form of an n -order square matrix , and its value is n ! sum of terms
In the formula, k 1 , k 2 ,..., k n is a sequence obtained by exchanging the element order of the sequence 1, 2,..., n for k times, and the Σ number represents the pair of k 1 , k 2 ,... ., k n take all the permutations of 1, 2, ..., n and sum up, then the number D is called the corresponding determinant of the n -order square matrix . For example, the fourth-order determinant is 4 ! The sum of terms of the form , and where a 13 a 21 a 34 a 42 corresponds to k = 3, that is, the symbol of the front end of the term should be
( -1 ) 3 .
If the n -order square matrix A = ( a ij ) , then the corresponding determinant D of A is written as
D =| A |=det A = det( a ij )
If the corresponding determinant of matrix A is D = 0 , A is called a singular matrix, otherwise it is called a non-singular matrix .
[ label set ] any k elements i 1 , i 2 ,..., i k in the sequence 1,2 ,..., n satisfy
1 ≤ i 1 < i 2 <...< i k ≤ n (1)
i 1 , i 2 ,..., i k form a subcolumn of {1,2,..., n } with k elements and {1,2,..., n } with k elements The totality of the sub-columns satisfying (1) is denoted as C ( n , k ), obviously C ( n , k ) has a total of sub-columns . Therefore C ( n , k ) is a label set with elements (see twentieth Chapter 1, §1 , ii), C ( n , k )
The elements of σ , τ ,..., σ∈ C ( n , k ) are denoted by
σ ={ i 1 , i 2 ,..., i k }
is a subsequence of {1,2,..., n } that satisfies (1) . If τ ={ j 1 , j 2 ,..., j k } ∈ C ( n , k ), then σ = τ means i 1 = j 1 , i 2 = j 2 ,..., i k = j k .
[ Subform , main subform , cosubform , algebraic cosubform ]
Take any k rows and k columns ( 1 ≤ k ≤ n - 1 ) from the n -order determinant D , and the k -order determinant formed by the elements at the intersection of the k-row and k-column is called the k - order child of the determinant D formula, write
,
σ , τ ∈ C ( n , k )
If the selected k rows and k columns are the i 1 , i 2 ,..., i k rows and i 1 , i 2 ,..., i k columns, respectively, then the resulting k -order subformula is called Main subform . That is, when σ = τ ∈ C ( n , k ) , it is the main subform .
The n - k order determinant obtained by removing k rows (σ) and k columns ( τ ) from the determinant D is called the cofactor of the subformula, denoted as .
If σ ={ i 1 , i 2 ,..., i k } , τ ={ j 1 , j 2 ,..., j k } , then
is the algebraic cofactor of the subform .
In particular, when k = 1 , σ ={ i } , τ ={ j }, the subform is an element a ij , the cofactor of a ij is written as A ij , the algebraic cofactor of a ij is written as A ij , that is
and have ( 2 ) 
or ( 3 ) 
[ Laplace expansion theorem ] If any k rows ( 1 ≤ k ≤ n -1 ) are taken in the n -order determinant D , then all the k -order sub-formulas and their respective algebras contained in these selected rows The sum of the products of cofactors is equal to the determinant D , that is, for any σ∈ C ( n , k ) , 1 ≤ k ≤ n -1 ,
( 4 )
where ∑ represents the summation of all elements in the label set C ( n , k ) .
Laplace's theorem is done for rows, and similar results are obtained for columns
( 5 )
Furthermore
( 6 )
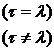( 7 )
Obviously ( 2 ), ( 3 ) are special cases of ( 6 ), ( 7 ), respectively .
[ Laplace's identity ] Let A =( a ij ) m ′ n , B =( b ij ) m ′ n ( m ≥ n ), and let l = , 
all n -order subformulas of A are U 1 , U 2 , ... , U l , and the corresponding n -order subformulas of B are V 1 , V 2 , ..., V l , then
det( A τ B )=
2. The nature of the determinant
1 ° ï A 1 A 2 L A m ï = ï A 1 ï ï A 2 ï L ï A m ï
ï A m ï = ï A ï m , ï kA ï = k n ï A ï
In the formula, A 1 , A 2 , L , and A m are all square matrices of order n , and k is any complex number .
2 ° After the row and column are interchanged , the value of the determinant remains unchanged, that is,
| |=| A |
where represents the transposed matrix of A (see § 2 of this chapter ) .
3 ° Interchange any two rows (or columns) of the determinant, change the sign of the determinant . For example
=
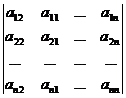4 ° Multiplying a row (or column) of the determinant by the number α is equivalent to multiplying the determinant by the number α . For example
= a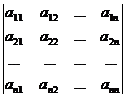
5 ° Multiply one row (or column) element of the determinant by the number α and add it to the corresponding element in another row (or column), the value of the determinant does not change . For example
=
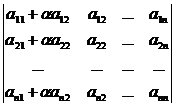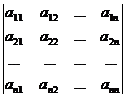
6 ° If a row (or column) of the determinant is all zero, then the determinant is equal to zero .
A determinant is zero if two rows (or columns) of the determinant have identical or proportional elements .
A determinant is zero if a row (or column) of elements in the determinant is a linear combination of corresponding elements in some other row (or column) .
7 ° If all elements of a row (or column) in the determinant can be expressed as the sum of two terms, the determinant can be expressed by the sum of two determinants of the same order . For example
= +
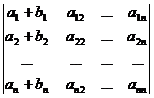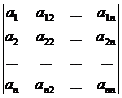
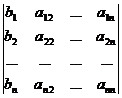
3. Several special determinants
[ diagonal determinant ]
=
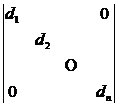[ triangle determinant ]
=
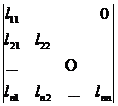[ Second-order determinant ]
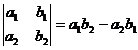
[ third-order determinant ]
= + + 
— — —
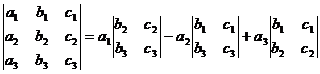
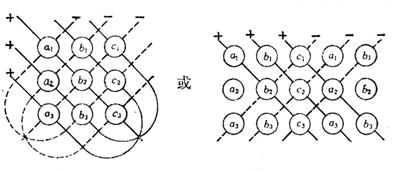
memory method
The value of the determinant is equal to the sum of the products of the elements on the solid lines minus the sum of the products of the elements on the dotted lines .
[ fourth-order determinant ]
= 
- + -
= 
- +
+ 
- +
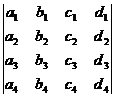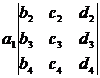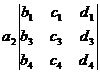
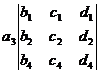
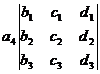
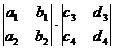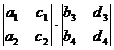
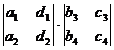
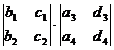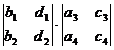
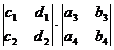
Note that the fourth-order and higher-order determinants cannot use the memory method of the third-order determinant, and should be expanded according to the Laplace expansion theorem by the method of step-by-step reduction .
[ Vandermonde determinant ]
=
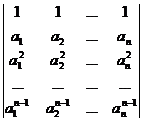where Õ is the product of all pairs ( i , j ) ( 1 ￡ j < i ￡ n ) .
[ Reciprocal symmetric determinant ]
=
