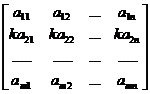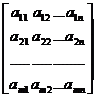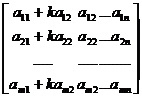§2 Matrix operations

 

1. Equality, addition, subtraction, multiplication, multiplication, transposition and conjugation of matrices

 

operations and their rules	Properties and Description
[ equal ] = if and only if	Equal matrices must have the same number of rows and columns .     Two matrices are equal, which means that the elements at each corresponding position are equal .
[ addition and subtraction ] ±                    = in	Only matrices of the same type can be added and subtracted (the elements of each corresponding position are added and subtracted) . A + B = B + A      ( commutative law ) ( A + B ) + C = A + ( B + C )                  ( associativity )
[ multiplication ] =	When multiplying a matrix, multiply the number to each element of the matrix . kA = Ak k ( A + B ) = kA + kB ( k + l ) A = kA + lA k ( lA )=( kl ) A ( k , l are any two complex numbers )
[ multiplication ] if   A =( a ij ) is an m ′ n matrix   B = ( b ij ) is an n ′ s matrix , then   AB =( a ij ) ( b ij )=( c ij )= C where C is an m ′ s matrix, and c ij =                    operations and their rules	The element c ij of the product is equal to the multiplication of the i -th row of the left matrix and the corresponding element of the j -th column of the right matrix and then added . The number of columns of the left matrix must equal the number of rows of the right matrix . ( AB ) C = A ( BC )     ( associative law )    k ( AB )=( kA ) B = A ( kB )       ( k is any complex number ) [ Note ] AB = BA does not hold in general, that is, there is no commutative law .    Properties and Description
[ Transpose ] The n ′ m matrix obtained by exchanging the columns and rows of the m ′ n matrix A = ( a ij ) is called the transpose matrix of A , which is denoted as      =	( A + B ) t = A t + B t ( kA ) t = kA t ( k is any complex number ) ( AB ) t = B t A t ( reverse order law ) ( A 1 A 2 ... A s ) t = ( A k ) t = ( A t ) k ( k is an integer )
[ Conjugate ] The matrix obtained by replacing all the elements of the matrix A =( a ij ) with their conjugate complex numbers is called the conjugate matrix of A , denoted as , ie                   = ( )	( k is any complex number )

 

2. Elementary transformation of matrices and elementary matrices

 

Let I = , which is called the identity matrix .

elementary transformation	elementary matrix	The relationship between elementary matrices and elementary transformations
The i -th column (or row) of the matrix intermodulates with the j -th column (or row)                                   elementary transformation	The matrix obtained by performing this elementary transformation on the unit matrix I is called an elementary matrix, denoted as I ij                         elementary matrix	Applying this elementary transformation to a matrix A is equivalent to multiplying A right (or left) by the elementary matrix I ij . For example             The relationship between elementary matrices and elementary transformations
Multiply the ith column (or row) of the matrix by the number k ( 1 0 )	The matrix obtained by performing this elementary transformation on the identity matrix I is called an elementary matrix, denoted as P i ( k )           P i ( k )=	Applying this elementary transformation to matrix A is equivalent to multiplying A by the elementary matrix P i ( k ) right (or left) . For example P 2 ( k ) A =    =
The ith row (or column) of the matrix plus k times the jth column (or row)	The matrix obtained by performing this elementary transformation on the unit matrix I is called an elementary matrix, denoted as A ij ( k )            A ij ( k )=	Applying this elementary transformation to a matrix A is equivalent to multiplying A by the elementary matrix A ij ( k ) right ( or left) . For example AA 12 ( k )=            =

Elementary transformations have the properties:

1 ° Any matrix  ( a _ij ) can be transformed into a diagonal matrix by a finite number of elementary transformations

( a _ij ) ®

The 2 ° elementary transformation does not change the rank of the matrix  .

 

3. Calculus of Matrix

 

       Assuming that the elements a _ij of the matrix A are all functions of the parameter t , then

   The derivative of a 1 ° matrix A is defined as 

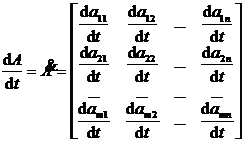
It is also possible to define higher-order derivatives of matrices .

    The integral of a 2 ° matrix A is defined as 

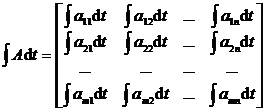
It is also possible to define multiple integrals of matrices .

 

Fourth, the special matrix

 

[ Zero matrix and zero factor ] A matrix whose   elements a _ij are all zeros is called a zero matrix , denoted as

O =( 0)=

A zero matrix has the properties:

O + A = A + O = A

OA = AO = O

A + ( - A ) = O , - A is called the negative matrix of A

       If A , B are non-zero matrices, that is, A 1 O , B 1 O , and AB = O , then matrix A is called the left zero factor of matrix B , and matrix B is the right zero factor of matrix A , for example

A = , B = 

AB = = = O

       [ Diagonal Matrix ] A square matrix   whose elements other than the main diagonal are all zeros ( d _ij =0, i 1 j ) is called a diagonal matrix, denoted as

D = =diag( d ₁ , d ₂ ,..., d _n )=[ d ₁ d ₂ ... d _n ]     

   Diagonal matrices have properties:

   1 ° left multiplied by B 

DB = =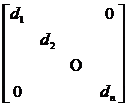

             =

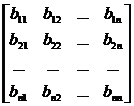
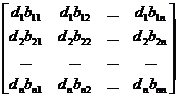
   2° right by B

BD = =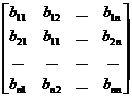

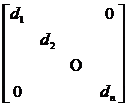
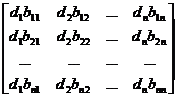
   3 ° The sum, difference and product of two diagonal matrices are  still diagonal matrices .

   [ Quantity matrix ] The diagonal matrix of d _i  = d ( i =1,2,..., n ) is called the quantity matrix, and is written as

D = =[ d d ... d ]          

       Obviously DB = BD = dB .

       [ identity matrix ] The quantity matrix with d  = 1 is called the identity matrix, denoted as

I = = 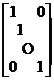" 1   1      ...     1 "

       Obviously IB = BI = B .

       [ Symmetric Matrix ]   Satisfies the condition

a _ij = a _ji       ( i , j =1,2,..., n )

The square matrix A = ( a _ij ) is called a symmetric matrix . For example

A =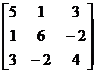

is a symmetric matrix . A symmetric matrix has the properties:

       If A and B are both symmetric matrices, then , and A ^{- 1} (matrix that makes A - ^{1 =} A - ^{1 A} = I. For details , see Section 6), A ^m ( m is a positive integer ) , A + B is still a symmetric matrix .

       [Real symmetric matrix] Real symmetric matrices can be divided into positive definite matrices, semi-positive definite matrices, negative definite matrices, semi-negative definite matrices and indefinite matrices according to their eigenvalues ​​(this section, VII). Their definitions and sufficient and necessary conditions are as follows

name	Definition	Necessary and sufficient conditions
positive definite matrix     positive semi-definite matrix       Negative definite matrix       Semi-negative definite matrix         indefinite matrix	A real symmetric matrix whose eigenvalues ​​are all greater than zero   A real symmetric matrix with all eigenvalues ​​less than zero   A real symmetric matrix whose eigenvalues ​​are all less than zero     A real symmetric matrix with none of the eigenvalues ​​greater than zero       Real symmetric matrix with eigenvalues ​​both greater and less than zero	All principals are greater than zero, i.e. A i >0    ( i =1,2,..., n )   det A =0 A i 3 0    ( i =1,2,..., n - 1)      ( =1,2,..., n )   det A =0      ( =1,2,..., n - 1 )   Either there is an even-order main subform A 2 k =0, or there are two odd-order main subforms, one of which is positive and the other is negative

       [ Antisymmetric matrix ]   Satisfies the condition

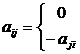
          ( i , j =1,2,..., n )

The square matrix A = ( a _ij ) is called an antisymmetric matrix . For example

A =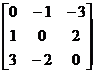

is an antisymmetric matrix . An antisymmetric matrix has the properties:

    1 °   If A , B are both antisymmetric matrices, then A ^τ = - A , and A ^{- 1} , A + B are still antisymmetric matrices,

^Am is _    

    2 °   Any square matrix A can be decomposed into the sum of a symmetric matrix B = ( b _ij ) and an antisymmetric matrix C = ( c _ij ) , namely

A = B + C

just take

b _ij =( a _ij + a _ji ), c _​​ij =( a _ij - a _ji )    

( i , j =1,2,... n )

    [ Hermitian matrix ]   satisfies the condition

^At = _

The square matrix A of is called the Hermitian matrix . For example

A =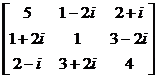

is the Hermitian matrix . The Hermitian matrix has the properties:

    If A and B are both Hermitian matrices, then A + B is still a Hermitian matrix . If A is a real square matrix (that is, a _ij is all real numbers), then A is a symmetric matrix .

       [ Anti-Hermitian matrix ]   satisfies the condition

^At = _

The square matrix A of is called the anti-Hermitian matrix . For example

A =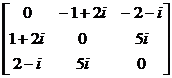

is the anti-Hermitian matrix . The anti-Hermitian matrix has the properties:

       If both A and B are anti-Hermitian matrices, then A + B is still an anti-Hermitian matrix . If A is a real square matrix, then A is an anti-symmetric matrix .

       [ Orthogonal Matrix ]   Satisfies the condition

^At = _

The square matrix A of is called an orthogonal matrix . For example

A =

is an orthogonal matrix . An orthogonal matrix has the properties:

       If A = ( a _ij ) and B are orthogonal matrices, then

   1 °  , AB is still an orthogonal matrix .

   2 °   det A = ± 1.

   3°      

                

       [ Unitary ( U ) matrix ]   Satisfies the condition

The square matrix A of is called a unitary ( U ) matrix . For example:

A =

is a unitary matrix . A unitary matrix has the properties:

       If A = ( a _ij ) and B are unitary matrices, then

    1 ° A  ^-1 , AB is still a unitary matrix .

    2 °   det A · det =1.

    3 ° If ​​A is a real square matrix  , then A is an orthogonal matrix .

       [ Strip matrix ]   Satisfies the condition

a _ij = 0    

The square matrix A = ( a _ij ) is called the band matrix . 2 m +1 is called the bandwidth . The general form is

A =

       [ Triangular Matrix ]   Satisfies the condition

a _ij = 0  ( i > j )

The square matrix A = ( a _ij ) is called an upper triangular matrix, and the general form is

                              A =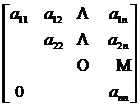

To meet the conditions

                            

The square matrix of is called a lower triangular matrix, and the general form is

B =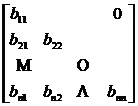

       A triangular matrix has the properties:

       1 ° When the main subforms of the first r order of any square matrix C of rank r are not 0  , C can be expressed as the product of an upper triangular matrix A and a lower triangular matrix B , that is,

C = AB

       2 °  The sum , difference , product and multiplication of upper (or lower) triangular matrices are still upper (or lower) triangular matrices .

       [ Blocked matrix ]   The array of elements in matrix A is divided into small blocks (called subarrays) with horizontal and vertical dashed lines , and A becomes a block matrix . For example

A = =

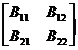
in the formula

                 B ₁₁ = 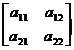, B ₁₂ =

                        B ₂₁ = , B ₂₂ = 

They are all subarrays of A.

       When performing operations on block matrices, subarrays can be treated as elements of normal matrices . These operations include addition , subtraction , multiplication , multiplication , transposition, and conjugation .

       [ Block Diagonal Matrix ]   The sub-matrixes on the main diagonal are all square matrices , and the block matrix in which the rest of the sub-matrixes are zero matrices is called a block diagonal matrix . The general form is

A =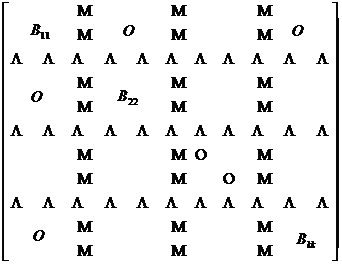

The inverse matrix A ^{- 1} of the block diagonal matrix A and the determinant of A can be obtained by the following simple formula

A ^{- 1} =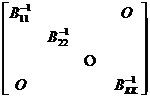

det A = det B ₁₁ · det B ₂₂ · ... · det B _kk

       Note that the determinant of a general block matrix cannot be calculated by using a method that treats a subarray as an element of a normal matrix, such as converting a fourth-order square matrix into a block matrix

A = =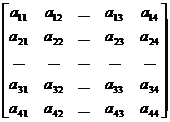

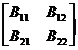
In general det A = det B ₁₁ · det B ₂₂ - det B ₂₁ · det B ₁₂ does not hold (see fourth-order determinants in §1 , 2, 3 ) .

 

5. Similarity Transformation

 

       [ Similar transformation ]   If there is a non-singular matrix X (ie det X 1 0 ) such that

B = AX

Then the matrix A is said to be similar to the matrix B , and it is also said that A is transformed into B by similar transformation , denoted as A ~ B. It has the following properties:

       1 ° A  ~ A , ^At ~ A . _

       2 ° If A  ~ B , then B ~ A .

       3 ° If ​​A  ~ C , B ~ C , then A ~ B .             

       4° ( A ₁ + A ₂ +...+ A _m ) X = A ₁ X + A ₂ X + ...+ A _m X   

       5° ( A ₁ A ₂ ... A _m ) X = A ₁ X    · A ₂ X · ... · A _m X

       6 °   A ^m X = ( AX ) ^m

          If 7° is a polynomial of matrix A , then

X =

       8 ° If A  ~ B , then

       A and B have the same rank, i.e. rank A = rank B .

      The determinant of A and B is the same, that is, det A = det B .

      The traces of A and B (as defined in this section, VII) are the same, i.e. tr A = tr B .

      A and B have the same characteristic polynomials and eigenvalues ​​(this section, seven) .

      [ Orthogonal transformation ] If Q is an orthogonal matrix (ie = Q ^t ) , then it is called

Q ^t AQ

is the orthogonal transformation of matrix A , and its properties are similar to similar transformations . In particular, there are properties:

A symmetric matrix A is still a symmetric matrix after orthogonal transformation .

[ Rotation Transformation ]   Take the orthogonal matrix U as

                                                          

U _pq =( u _ij )=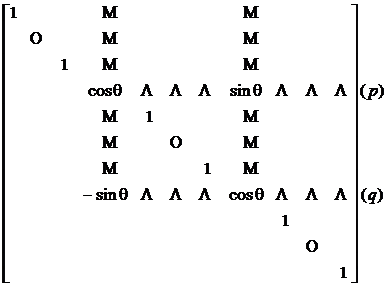

 

which is

u _pp = u _qq =

u _pq = -u _qp =

  u _ii = 1         ( i 1 p,q )

                                  u _ij = 0      ( i, j1p ,q ; i1j )

at this time called

B =

 

is the rotation transformation of A , q is called the rotation angle, if A is a symmetric matrix, then the element b _ij of B and the element a _ij of A have

The corresponding relationship is as follows:
               

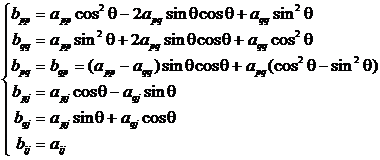
Also has properties:          

=

       If the rotation angle is taken

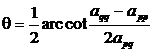
Then the rotation transformation makes

 

6. Inverse matrix

 

      [ Inverse matrix and its properties ]   If the square matrix A , B satisfies the equation

AB=BA=I    ( I is the identity matrix )

Then A is called the inverse matrix of B , or B is called the inverse matrix of A , denoted as

A= or B=  

At this time , both A and B are called invertible matrices (or non-singular matrices, or full-rank matrices) . Otherwise, they are called irreversible matrices (or singular matrices, or reduced-rank matrices) .

Invertible matrices have properties:

1 ° If A and B are invertible matrices  , then AB is still an invertible matrix, and

     (reverse order law)

In general, if A ₁ , A ₂ ,...,A _s are invertible matrices, then

       A necessary and sufficient condition for a 2 ° matrix A to be invertible is  : det A 1 0.

       3 ° If ​​the matrix A is invertible  , then

det 1 0 and det = (det     

= A , ( a              1 0)

=( ) ^t ,           

       The necessary and sufficient condition for matrix A to be invertible at 4 °  is that the eigenvalues ​​of matrix A are all non-zero .

       [ Expression of Adjoint Matrix and Inverse Matrix ]   Let A _ij be the algebraic cofactor of the element a _ij of the i -th row and the j -th column of the matrix A =( a _ij ) , then the matrix

A ^* =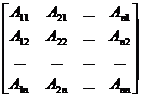

is called the adjoint matrix of matrix A.

       If A is a non-singular matrix, that is, det A 1 0, then the inverse matrix expression of A is

       Note that the element at row i , column j of A ^* is the algebraic cofactor of the element at row j , column i of A.

       [ Inverse of Diagonal Matrix ]   Diagonal Matrix

D = , d _i      1 0    ( i =1 ,2 ,..., n )

The inverse matrix of is

D ^{- 1} =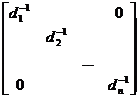

       Obviously the inverse of a diagonal matrix is ​​still a diagonal matrix .

       [ the inverse of a triangular matrix ]   a triangular matrix

L = ,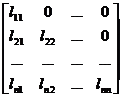         

The inverse matrix of is

= P =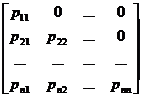

in the formula

              ( i =1 ,2 ,..., n )

           

                     

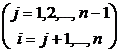
       Obviously the inverse of a non-singular lower (upper) triangular matrix is ​​still a lower (upper) triangular matrix .

       [ inverse of a positive definite matrix ]

       1 ° Gauss  -Jordan

       The inverse A ^{- 1} =( b _ij ) of a positive definite matrix A =( a _ij ) can be obtained by the following recursive formula:

, ,             

         

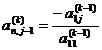
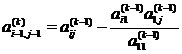
                                         ( k=1 ,2 ,...,n )

finally got

where n is the order of the positive definite matrix A.

       The steps of the 2 ° triangular matrix method    are as follows:

       ( 1 ) Express the positive definite matrix A = ( a _ij ) as

A = L D L ^t

where D is a real nonsingular diagonal matrix

D =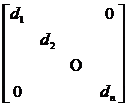

L is a real nonsingular lower triangular matrix.

L =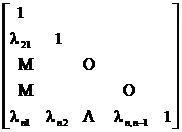

L ^t isthe transpose matrixof L. d _i ( i =1,2,..., n ) and l _ij ( i =2,..., n;j=1,...,n )are recursively as follows The formula calculates:

        

         

                

                   

          

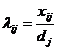
       ( 2 ) Find the inverse matrix of D

=

       ( 3 ) Find the inverse matrix of L

=

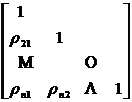
in the formula

     

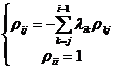
       ( 4 ) Find the inverse matrix of A

=( L D =( ) ^t

=

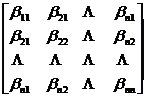
in the formula

               

       Note that this method has the advantage of avoiding the square root operation .

       [ The inverse of the block matrix ]   Let the block matrix of a non-singular matrix A be

A =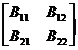

In the formula, B ₁₁ , B ₂₂ are square sub-matrixes, then the inverse matrix of A

A ^{- 1} =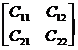

It is calculated by the following formula

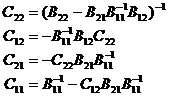
       [ Elementary transformation method to find the inverse matrix ]   Let

= = = B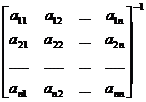

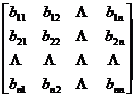
pair matrix

Do a series of elementary transformations of rows, so that the left block of the dotted line becomes a unit matrix, and the right block becomes the inverse matrix of A B = A ^{- 1} , that is

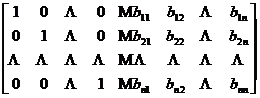
       [ Approximate method for inverse matrix ] is   set as the initial approximate inverse matrix of matrix A , and a more accurate inverse matrix can be obtained by the following iterative formula:

          ( n= 0 ,1,2 , ... )

where I is the identity matrix of the same order as A.

       [ Test matrix for computer inversion program ]   Use the following n -order nonsingular matrices and their inverses to test the computational program for the inversion of large matrices .

A =

=

 

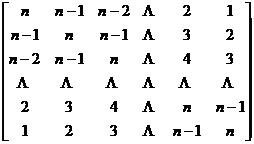
Seven,   eigenvalues ​​and eigenvectors

 

       [ eigenvalue and eigenvector ]   for n -order square matrix

 

A =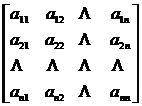

and an n -dimensional nonzero column vector

=( a ₁ ,a ₂ ,..., ^an ) _t

If there is a number λ such that

A α = λα

Then λ is called the eigenvalue (eigenroot) of matrix A, and α is the eigenvector corresponding to the eigenvalue λ of matrix A.

       The one with the largest absolute value among all the eigenvalues ​​of matrix A is called the first eigenvalue of A.

       [ Characteristic matrix · Characteristic polynomial · Characteristic equation ] nth  -order square matrix

A =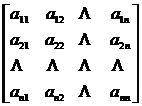

The feature matrix of is defined as

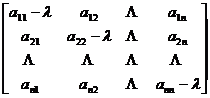
where I is a unit matrix of order n . The determinant | A - λ I | is called the characteristic polynomial of the matrix A , denoted as

j ( l )=| λI | _

equation

j ( l )=0

is called the characteristic equation of matrix A.

       [ The trace and spectrum of the matrix ]   The sum of the elements on the main diagonal of the nth -order square matrix A is called the trace of A , and is written as

       The n roots l ₁ , l ₂ , ... , l _n of the characteristic equation j ( l ) = 0 are the n eigenvalues ​​of the matrix A. The set { l ₁ , l ₂ , ... , l _n } is called The spectrum of matrix A , denoted ch A .

       Linear Homogeneous Equations

The non-zero solution a is the eigenvector corresponding to the eigenvalue _li of matrix A.

       [ Properties of Eigenvalues ​​and Eigenvectors ] 

       1 ° Let   l ₁ , l ₂ , ... , l _n be the n eigenvalues ​​of the n -order square matrix A , then

          The eigenvalues ​​of A ^k ( k is a positive integer) .

          The eigenvalues ​​of the inverse matrix A ^{- 1 of} A are .

      The eigenvalues ​​of the adjoint matrix A ^* of A are .

         The sum of n eigenvalues ​​of 2° n -order square matrix A is equal to the trace of A, and the product of n eigenvalues ​​of matrix A is equal to the determinant of A, that is ,

l ₁ + l ₂ +...+ l _n = a ₁₁ + a ₂₂ +...+ a _nn

               l ₁ l ₂ ... l _n =

From this, it can be deduced that another sufficient and necessary condition for the invertibility of the matrix is ​​that all eigenvalues ​​of A are not zero .

       3 ° If  ​​li is the _k multiple roots of the characteristic equation , the number of linearly independent eigenvectors corresponding to li is not greater than k. When li _is a single root , _there is only one linearly independent eigenvector corresponding to _li .

       The eigenvectors corresponding to different eigenvalues ​​of the 4 ° matrix A  are linearly independent .

       若n阶方阵A对应于特征值l₁，l₂，...，l_s的线性无关的特征矢量分别有k₁,k₂,...,k_s个，则这个特征矢量线性无关，且.

    5°  实对称矩阵的特征值都是实数，并且有 n个线性无关（而且是正交）的特征矢量.

       6°  矩阵的特征值在相似变换下保持不变，特别，A^t与A具有相同的特征值.

       [求第一特征值的迭代法]  在实际问题中，往往不要求算出矩阵A的全部特征值，只需算出第一特征值，用迭代法计算如下：

              

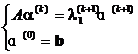
       Assuming that at that time , it can be considered that a ^{( k )} ≈ a ^{( m +1)} , then iterate to it . At this time , it is the approximate value of the first eigenvalue of matrix A , and a ^{( m +1)} is the corresponding eigenvector .

       [ Jacobi Method for Real Symmetric Matrices ] Suppose the eigenvalues ​​of n -order real symmetric matrix A =( a _ij ) are l ₁ , l ₂ , ... , l _n , then there must be an orthogonal matrix Q such that

Q ^t AQ =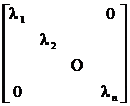

is a diagonal matrix . The orthogonal matrix Q can be approximated by the product of a series of rotation matrices:

Q =

in the formula

                    

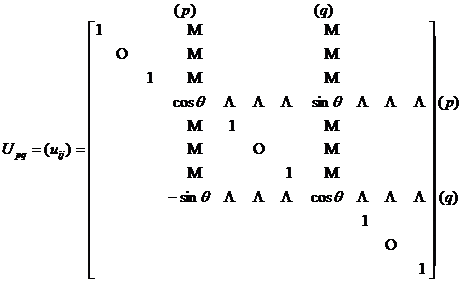
Pick

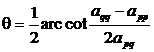
       Because under this rotation transformation, the elements located at the intersection of the pth row and the qth column ( p 1 q ) in the matrix are eliminated (see this section, five), while the sum of the squares of all the elements of the matrix remains unchanged, and the diagonal The sum of squares of the elements on the line increases, so the sum of squares of the off-diagonal elements decreases. Therefore, when the number of rotations is large enough , the absolute value of the off-diagonal elements can be made small enough . For a given The accuracy of e > 0 , if | a _ij | < e ( i 1 j ), then a _ij ≈ 0. Then a specific iterative method for finding the eigenvalues ​​and eigenvectors of matrix A is obtained .

       1 ° Find the eigenvalues  ​​l ₁ , l ₂ , ... , l _n according to the following recursive formula :

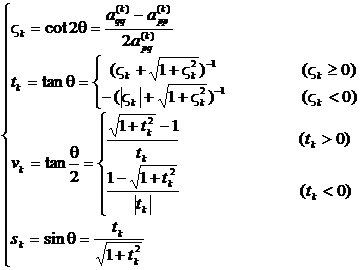
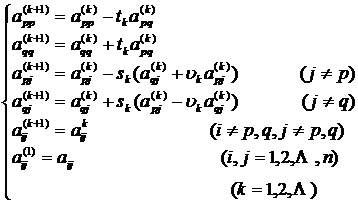
       Assuming that at that time , it can be considered that it can be iterated to . And take it as an _{approximate value of} li :

       2 ° to find the eigenvectors    from 1° have

 

=

remember

P _m =U _1… U _{m- 1} U _m

 

but

AP _m = P _m

So P _m is the eigenvector matrix .

       P _m is calculated by the following recursive formula:

 

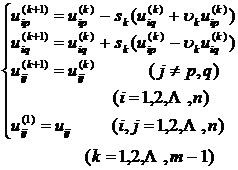
finally got     

 

which is          

 

is an approximation of the eigenvector _{corresponding} to the eigenvalue li .

       [ Methods for finding eigenvalues ​​of symmetric tridiagonal matrices ]

       The 1 ° similarity transformation method   sets A to be a symmetric tridiagonal matrix of order n :

 

                            A = (1)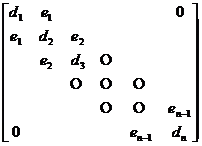                              

After similarity transformation

 

 

where I is the identity matrix , t _k is an appropriately selected constant, and U _i is the Jacobian rotation matrix:

is the transposed matrix of _U i _. And A 1 ₌ A , A k _{+1 is} similar to I _, and A _m is similar to . Therefore , if the eigenvalue of A _m is ,2 ,...,n ) is

                      ( i =1 ,2 ,…, n )

       Assuming that at that time , it can be considered that s _i and c _i can be appropriately selected so that when m is sufficiently large, A _m can be transformed into a diagonal matrix with this precision; its eigenvalues .

        ( i=1 ,2 ,...,n ) can be calculated by the following recursive formula:

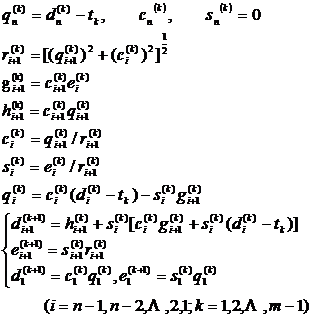
       The choice of t _k has a great influence on the convergence speed, and t _k is taken as the second-order matrix

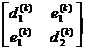
, which is close to the eigenvalue of , i.e.

tk ₌ _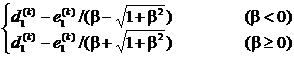

in the formula                         

       2 ° bisection method   Let A be an n -order symmetric tridiagonal matrix (such as ( 1 )), for any l , let the sequence

q ₁ ( l ) = d ₁ - l

q _i ( l )=

The number of q _i ( l )<0 in these relations is N ( l ) ( in these relations, for some i , if q _{i -1} ( l )=0 , just replace it with an appropriately small number ), then N ( l ) is equal to the number of eigenvalues ​​of matrix A less than l .

Assuming that the k -th eigenvalue l _k ( l ₁ ≤ l ₂ ≤ … ≤ l _k ≤ … ≤ l _n ) of matrix A is in the interval [ u , ] , let , when N ( r ₁ ) ≥ k , then l _k Î [ u , r ₁ ] ; when N ( r ₁ )< k , then l _k Î [ r ₁ , v ];… and so on, after m steps, l _k is included in the interval of width . When m is sufficiently large, the desired eigenvalue can be obtained .

 

Eight, matrix polynomial and minimum polynomial

 

      [ Matrix polynomial ] Let ( i = 1,2,...,n ) be a number in a certain number field (real number field or complex number field), and A is an n -order square matrix on this number field , then the expression

f ( A )= a ₀ I+a ₁ A+...+a _n A ⁿ

is called the polynomial of the matrix A , where I is the identity matrix of order n .

       If the matrix A is such that

f ( A ) =O

Then call A a polynomial

f ( l ) = a ₀ l + a ₁ l + ...+a _n l ⁿ

's root .

       [ Hamilton - Cayley theorem ] Any square matrix is ​​the root of its characteristic polynomial .

       [ Minimum polynomial and its properties ] In the non-zero polynomial f ( l ) with matrix A as the root, there is a polynomial j ( l ) with the leading coefficient of 1 and the lowest degree , which is called the minimum polynomial of matrix A.

       The smallest polynomial has the property:

       1 ° Any square matrix has only one minimum polynomial  ;

       2 ° Any polynomial f  ( l ) with A as the root can be divisible by the smallest polynomial j ( l ) of A. In particular, the smallest polynomial of any square matrix can divide its characteristic polynomial;

       The roots of the characteristic polynomial of a 3 ° square matrix A are all the roots of the smallest polynomial of A  :

       4 ° Similar matrices have the same characteristic polynomial and minimum polynomial  .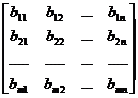
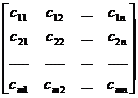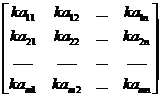
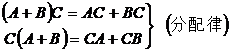
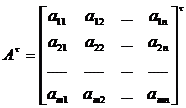
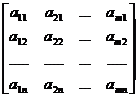
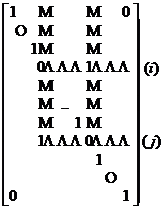
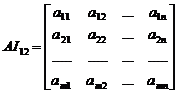
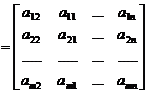
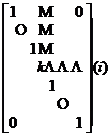
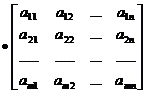