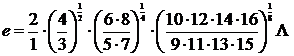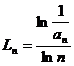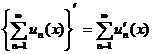§2 Convergence and operation of series
1. Discriminant method for convergence of numerical series
1 . Basic Concepts and Basic Properties
[ Basic concept of series ] Let , , be an infinite sequence , the symbol
It is called an infinite series , abbreviated as a series , and denoted as . a n is called the general term of the series .
A n = a 1 + a 2 + ( n =1, )
is called the nth partial sum of the series . If when n ∞ , the partial sum sequence { A n } has a finite or infinite (but definite positive or negative sign) limit A :
A = A n =
Then A is called the sum of series and written as
A = a 1 + a 2 +
A series is said to be convergent if it has a finite sum, otherwise it is said to be divergent if the series sum is equal to ±∞ , or does not exist .
[ Basic properties of series ]
1 ° Discarding the finite term in front of the series or adding a finite term in front of the series does not affect the properties of the convergence and divergence of the series .
2 ° If the series converges, then the sum of the remainders after its mth term
a m = a m +1 + a m +2 +
tends to zero when m ∞ .
3 ° If the series converges and c is any constant, then the series also converges, and we have
= c
4 ° If both converge with and converge, then also converge, and have
= ±
[ Cauchy criterion ] The necessary and sufficient condition for series convergence is: for any ε > 0 , there is a positive integer N = N ( ε ), so that when n N , for all positive integers p , the following inequality holds:
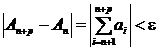
[ Necessary Condition for Series Convergence ] A necessary condition for series convergence is that the general term a n tends to zero, that is, a n =0.
2. Convergence discrimination method of series of the same number
Assume
(1)
with (2)
are two series with the same sign (that is, the series with the same sign for each item, when they are all positive, they are called positive-term series), and the convergence judgment method of such series is shown in the following table .
|
name |
condition |
Convergence of series |
||
|
converge |
divergent |
|||
|
comparative judgment |
I |
When n > N , 0 ≤ a n ≤ b n |
If series (2) converges, then series (1) converges |
If series (1) diverges, then series (2) diverges |
|
II |
( 0 ≤ K ≤ + ∞ ) ( b n ≠ 0) |
When K <+ |
When K > 0 , if series (2) diverges, then series (1) diverges |
|
|
III |
When n > N ,
( a n ≠ 0 , b n ≠ 0 ) |
If series (2) converges, then series (1) converges |
If series (1) diverges, then series (2) diverges |
|
|
IV |
When n → ∞ , a n ~ b n |
Series (1) and (2) converge simultaneously |
Series (1) and (2) diverge simultaneously |
|
|
V |
a n = O * ( ) |
when p > 1 |
when p ≤ 1 _ |
|
|
Dharambell's test |
a n >0( n =1,2,…) = q |
when q < 1 |
when q > 1 |
|
|
Cauchy's Discrimination |
a n ≥ 0 ( n = 1,2,…)
|
when q < 1 |
when q > 1 |
|
|
Arab Judgment |
a n > 0( n =1,2,…)
|
when p > 1 |
when p < 1 |
|
|
Gaussian discriminant |
a n > 0( n =1,2,…)
|
when λ > 1 , or when λ =1 and μ > 1 |
when λ < 1 , or when λ =1 and μ ≤ 1 |
|
|
Cauchy Integral Discrimination Method |
f ( x ) ( x ≥ 1 ) is a non-negative non-increasing function |
Convergence at the same time |
Divergence at the same time |
|
|
logarithmic discriminant |
a n > 0( n =1,2,…) Assume |
When n > N ( )
|
When n ≥ N ( )
|
|
= p
3. Convergence method of sign-changing series
[ Absolute convergence of series ] If the series
(3)
Convergence, then the sign-change series (that is, the series in which positive and negative terms can appear arbitrarily)
(4)
also converges, and the series ( 4 ) is said to be absolutely convergent .
If the series ( 4 ) converges and the series ( 3 ) diverges, then ( 4 ) is said to be conditionally convergent (non-absolutely convergent) .
To determine the absolute convergence of a series, it is only necessary to apply the above convergence criterion for series of the same sign to a series with positive terms . But we must be careful about the divergence criterion. Although the series is divergent, the series is still It can be convergent (not absolutely convergent), with the exception of Cauchy's method and D'Alembert's method .
The sum of absolute convergent series is equal to the sum of all positive terms of the series minus the sum of the absolute values of all negative terms of the series .
[ Riemann's theorem ] is set as a .
[ Dallembell's Discrimination Method ] If the sign-change series satisfies the condition
= l
Then when l < 1 , it converges absolutely; when l > 1 , it diverges .
[ Leibniz discriminant ] If the interleaved series
Satisfy the condition: ( i ) c n ≥ c n +1 ( n =1,2,…),( ii ) c n = 0, then the series converges (generally speaking, non-absolute convergence) . For the series of remainder
There are the following estimates:
And the sign of the remainder is the same as that of the first item, and its absolute value is smaller than the absolute value of the first item .
[ Dirichlet's test ] If the partial sum A n = bounded, and when n , b n monotonically tends to zero, then the series converges .
[ Abelian discriminant method ] If the series converges and the numbers b n ( n =1,2,…) form a monotone bounded sequence:
| b n | ≤ K ( n =1 ,2 ,…)
Then the series converges .
2. The discriminant method for the convergence of function term series
1. Convergence and Uniform Convergence
[ Convergence and Convergence Region ] Assuming that u n ( x ) ( n = ) 
are all functions defined on a certain interval [ a , b ] , then it is called
is the series of function terms defined on [ a , b ] . If the partial sum of each point on the interval [ a , b ]
S n ( x )=
When n → ∞ , there is a limit S ( x ) , that is
S n ( x ) = = S ( x )
Then the function term series is said to be convergent on the interval [ a , b ] , the function S ( x ) is its sum, and the interval [ a , b ] is the convergence region .
r n ( x )=
is called the remainder . Obviously at each point x on the convergent region , there is
r n ( x )=0
That is to say, for any given ε > 0 and every point x on the convergence region [ a , b ] , there is a natural number N ( ε , x ) ( the size of N is not only related to the given positive number ε , And it is related to the value of x ) , so that when n ≥ N , there are
| r n ( x )|< ε or | |< ε
[ Consistent convergence ] Let the function term series
converges for every point on the interval [ a , b ] whose sum is S ( x ).
If for a given ε 0 , there is a natural number N ( ε ) that is only related to ε but not related to the value of x , so that when n ≥ N , the inequality
| r n ( x )|< ε or | |< ε
For all x on [ a , b ] is true, then the function term series is said to converge uniformly on the interval [ a , b ] , that is, the partial sum S n ( x ) converges uniformly to the sum of the series S ( x ).
From the definition of uniform convergence, it can be seen that the uniform convergence of the function term series on a certain interval [ a , b ] is higher than that on [ a , b ] point-to-point convergence . A function term that uniformly converges on a certain interval [ a , b ] The series converges point by point on [ a , b ] , but the series of function terms that converge point by point on the interval [ a , b ] does not necessarily converge uniformly on [ a , b ] .
2. Uniform convergence criterion
The necessary and sufficient conditions for the [ Cauchy criterion ] series to converge uniformly on the interval [ a , b ] are:
For any given ε > 0 , there exists a natural number N = N ( ε ) that is only related to ε but not related to x , such that when n N , the inequality
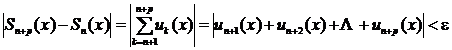
It holds for all natural numbers p and all points x on the interval [ a , b ] .
[ Weierstrass Discrimination Method ] For series , if there is a convergent numerical series , such that for all points x on the interval [ a , b ] , the inequality
is established, then the series converges absolutely and uniformly on the interval [ a , b ]
[ Abelian discriminant ] If the series converges uniformly on the interval [ a , b ] , the function sequence { ( x )} is monotonic for every x and bounded for any x and n :
|
then the series
( x )
Converges consistently over the interval [ a , b ] .
[ Dirichlet's test ] If the partial sum of the series is bounded for any x and n :
The sequence of functions { v n ( x )} (for each x ) is a monotonic sequence uniformly tending to zero over the interval [ a , b ] . Then the series
( x )
Converges consistently over the interval [ a , b ] .
3 . The operation of function series and its conditions
|
operation |
expression |
condition |
|
series and continuity |
|
( i ) ( ii ) |
|
Add and subtract item by item |
= ( a ≤ x ≤ b ) |
|
|
multiply |
= in ( a ≤ x ≤ b ) |
|
|
item-by-item limit |
= ( a ≤ ≤ b ) |
( i ) ( ( ii ) uniformly converges on [ a , b ] |
|
Item-wise differentiation |
( a ≤ x ≤ b ) |
( i ) And there are continuous derivatives , ( ii ) converges on [ a , b ] , ( iii ) |
|
Point-by-point points |
=
= Consistently holds for all points x on [ a , b ] |
( i ) continuous on [ a , b ] ( or integrable ) , ( ii ) uniformly converges on [ a , b ] |
Three , double series
[ Double series ] Known infinite set of numbers determined by two natural number indices
Arrange them in the shape of an infinite matrix:
Such a matrix is called an infinite matrix with two indexed elements .
is called a double series .
Limited to the first m rows and first n columns, considering finite sum numbers
This sum is called the partial sum of the double series .
If there is a double limit
A =
This limit is finite or infinite (but has a definite positive or negative sign), then this limit is called the sum of the double series, denoted as
A =
A series is said to be convergent if it has a finite sum, otherwise, it is said to be divergent .
A necessary condition for the convergence of the double series is that the general term tends to zero, i.e.
=0
[ Cumulative series ] If you add up each row individually in an infinite matrix , you get the row series
Then add up all the row series (first by column and then by row), that is
It is called a cumulative series . If the entries of a given infinite matrix are added row by row and then column by column, the second type of cumulative series is obtained
If tired limit
=
exists, then the cumulative series is said to be convergent and has a sum . If the cumulative limit
=
exists, then the cumulative series is said to be convergent and has the sum .
[ Relation between double series and accumulative series ] If ( i ) the double series converges and ( ii ) the row series converges, then the accumulative series converges and has the same sum as the double series
= A =
Similar results are obtained for the second type of cumulative series (cf. §1 , 3, 2 ) .
[ Positive term series ]
1 ° , then the necessary and sufficient condition for the convergence of the series is that it is partially summed and bounded .
2 ° set , if three series
, ,
If one of the series converges, then the other two series also converge and have the same sum .
3 ° Let the double series and the simple series consist of the same terms . In this case, the convergence of one series can be deduced from the convergence of the other, and the sums of the two are equal .
[ Absolutely convergent series ]
1 ° If a series consisting of the absolute values of the series' terms converges, then the series also converges .
If the series converges, then the final series is called an absolutely convergent series . If the series converges, but the series diverges, then the final series is called a conditionally convergent series .
2 ° If the series is absolutely convergent, then the row (or column) series are all absolutely convergent . In addition, the series composed of the sum of the row (or column) series is also absolutely convergent, and has the same as the double series. and .
3 ° If a double series and a simple series are composed of the same terms , then the absolute convergence of one of them can be deduced from the absolute convergence of the other, and the sum of the two is equal .
The 4 ° absolute convergent double series is commutative , that is, the series still converges after arbitrarily changing its summation order, and has the same sum as the original series .
5 ° If the absolute value series of the cumulative series is a convergent series, then not only the cumulative series itself converges, but also the cumulative series converges, and the sum of the two is equal .
6 ° If the simple series is absolutely convergent, after arbitrarily arranging its terms in the shape of an infinite matrix with two indexed elements, the series can be replaced by the cumulative series or .
The basic concepts and properties of double series can be extended to multiple series .
4. Infinite Product
[ basic concept ] set
is a given infinite sequence , then the notation
= , q n ≠ 0 ( n =1, )
is called an infinite product .
is called a partial product . If the sequence of partial products { P n } has a finite or infinite (but definite positive or negative sign) limit as n → ∞
P n = P
Then P is called the value of the infinite product, denoted by
P = = , q n ≠ 0( n =1, )
If the infinite product has a non-zero finite value P , it is called convergent, otherwise it is called divergent . If P = 0 , it is called divergent from zero .
To make the value of an infinite product equal to zero, it suffices that one of the factors of the product is zero. In the following discussion, it is always assumed that q n ≠ 0 ( n =1, ).
is called the coproduct of infinite products .
[ Infinite Product Convergence Criterion ]
A necessary condition for the convergence of the 1 ° infinite product is:
π m =1 or q n =1
where π m = .
The necessary and sufficient condition for the convergence of the 2 ° infinite product is: the series converges . Let L be the sum of the previous series, then P = e L .
3 ° Let q n =1+ a n ( n =1,2,…) , for a sufficiently large n , if there is a n >0 ( or a n <0) , then = the necessary and sufficient conditions for convergence are: Numbers converge .
4 ° = Convergence if the series and the series converge at the same time .
A sufficient and necessary condition for a 5 ° infinite product or to have zero value is that the sum of the series or is .
In particular, the infinite product has zero value if an < 0 and the series diverges, or if the series converges and the series diverges .
The necessary and sufficient condition for the absolute convergence of the 6 ° infinite product is that the series is absolutely convergent .
[ Consistent convergence of infinite products of function terms ] If the sequence of functions
P m ( x )= ( m =1, )
Convergence uniformly, and the limit is not always zero, then the infinite product of function terms is called
Convergently converge .
If it converges uniformly on a certain interval, and , then the infinite product also converges uniformly on that interval .
[ Infinite Product Expansion ]
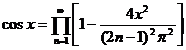
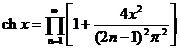
( | x | <1)
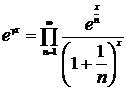( where γ is Euler's constant )
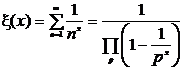
(where p runs over all prime numbers, ξ ( x ) is called the Riemann ξ function . )
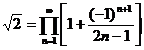
