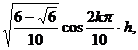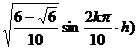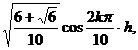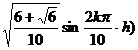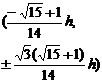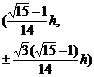§ 2 Multiple integration, curve integration and surface integration
One, multiple points
1. Double integral
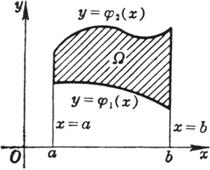
Double integral of continuous function f ( x , y ) in finite integrable plane region Ω
![]()
In the formula , , is the summation of all the subscripts i and j in Ω .![]()
![]()
![]()
![]()
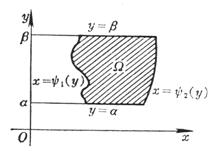
[ Calculation formula of double integral in a specific area ]
|
Integration area Ω |
|
|
|
set , then
|
[ Variable Substitution for Double Integrals ( Jacobian )] If a continuously differentiable function
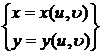
The single-valued bounded closed region Ω on the plane Oxy is mapped to the closed region Ω ' on the plane , and its Jacobian formula is![]()
![]()
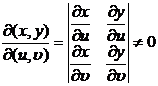
but
![]()
For example, if
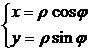
but
![]()
![]()
so
![]()
2. Triple Integral
[ Triple Integration in Cartesian Coordinates ] Suppose that the bounded region V is given by the following inequalities
a ≤ x ≤ b , ![]() ≤ y ≤ , ≤ z ≤
≤ y ≤ , ≤ z ≤![]()
![]()
![]()
Determine, where , , , are all continuous functions, and the function f ( x , y , z ) is continuous on V , then the triple integral of the function f ( x , y , z ) on the bounded region V![]()
![]()
![]()
![]()
![]()
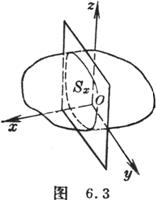
Sometimes the following formula is used to calculate:
![]()
where is the cross-section obtained by using a plane parallel to O yz to cross-section the area V ( Figure 6.3).![]()
For example , suppose V represents the closed area enclosed by the curved surface and the coordinate plane in the first trigram , then when all constants are positive, we have 

This type of integral is called a Dirichlet integral, and it is often used when computing multiple integrals .


[ Triple Integration in Cylindrical Coordinates ] ( Fig. 6.4)
![]()
(Generally, 0 ≤ ≤ 2 π )![]()
where V is the bounded region in Cartesian coordinates, and V ' is the expression of region V in the cylindrical coordinate system .
[ Triple Integration in Spherical Coordinates ] ( Fig. 6.5)
![]()
(Generally, 0 ≤ ≤ 2 π , 0 ≤ θ ≤ π )![]()
where V ' is the expression of the region V in the spherical coordinate system .
[ Variable Substitution for Triple Integral ( Jacobian )] If a continuously differentiable function
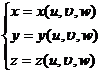
Map both sides of the bounded three-dimensional closed region of Oxyz space to the closed region V ' of O'u w space singularly , and when ( u , ,w ) ∈ V ' the Jacobian formula![]()
![]()
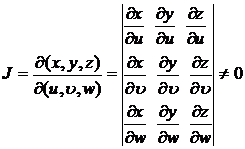
but
![]()
3. Multiple points
[ Direct calculation of multiple integrals ] If the function f ( ) is continuous in a bounded closed region Ω determined by the following inequalities :![]()
a ≤ ≤ b![]()
![]() ( )
( ) ![]() ≤ ≤ ( )
≤ ≤ ( )![]()
![]()
![]()
……………………
![]() ( )
( ) ![]() ≤ ≤ ( )
≤ ≤ ( )![]()
![]()
![]()
where a and b are constants, ( ) , ( ) ,…, ( ) , ( ) are continuous functions, then the corresponding multiple integrals can be calculated according to the following formula:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Variable Substitution for Multiple Integrals (Jacobian) ] If a continuously differentiable function
![]() = ( ), i =1 ,2 ,
= ( ), i =1 ,2 , ![]()
![]() … , n
… , n
The bounded closed region Ω in O space is mapped both sides into the bounded closed region Ω ' in O' space, and the Jacobian formula in the closed region Ω '![]()
![]()
![]()
but
![]()
In particular, according to the formula
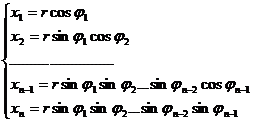
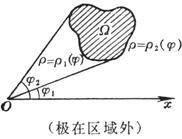
When transformed into polar coordinates ( r , ) , there are:![]()
![]()
2. Curve integral
|
|
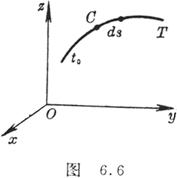
[ curve integral over arc length ] If the function f ( x , y , z ) is on a smooth curve C :
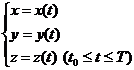
is defined and continuous at each point of (Figure 6.6 ) then
![]()
where d s is the differential of the arc, etc. This integral is independent of the direction of the curve C.![]()
[ Curve integral over coordinates ] If the functions P = P ( x , y , z ), Q = Q ( x , y , z ), R = R ( x , y , z ) on the smooth curve C:
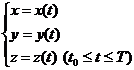
is continuous at each point of , and the positive direction of this curve is the direction of t increasing, then
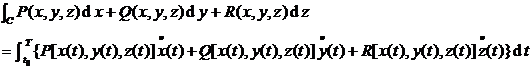
When the positive direction of curve C changes, the sign of the integral changes .
[ Total differential case ] If the function P = P ( x , y , z ), Q = Q ( x , y , z ), R = R ( x , y , z ) any smooth curve C in the region V on continuous, and
![]()
where u = u ( x , y , z ) is a single-valued differentiable function in the region V , then
![]()
In the formula ( ![]() ) is the starting point of the integral curve C , and ( ) is the end point of the integral curve C. This means that under the assumed conditions, the integral value has nothing to do with the shape of the curve C , but only the start and end points of the curve ( Figure 6.7).
) is the starting point of the integral curve C , and ( ) is the end point of the integral curve C. This means that under the assumed conditions, the integral value has nothing to do with the shape of the curve C , but only the start and end points of the curve ( Figure 6.7).![]()
Functions P , Q , R with continuous first-order partial derivatives in a simply connected region V can be expressed as total differentials
![]()
The necessary and sufficient conditions for is: in the region V the equation
![]()
is established . At this time, the function u can be obtained according to the following formula:
![]()
( ![]() ) is a fixed point in the region V.
) is a fixed point in the region V.
|
|
[ Green formula ]
The relationship between the 1 ° curve integral and the double integral . Let C be a simple (no self-intersection) closed curve that is smooth piece by piece, enclosing a single connected bounded region S , the direction of the line keeps the region S on the left , if The functions P ( x , y ), Q ( x , y ) and their first-order partial derivatives are continuous on S + C , then there is Green's formula :
![]()
|
|
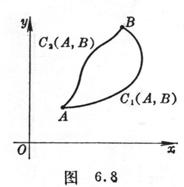
The relationship between the 2 ° curve integral and the integral line . If the functions P , Q , are continuous in the region S , and ![]()
![]()
Then the integral along any smooth closed curve in S is zero, i.e.
![]()
Thus the integral from A to B in S is circuit independent (Fig. 6.8) , i.e.
![]()
3.
Surface integral
[ Surface integral over surface area ]
1 ° if S is a piece-by-piece smooth bilateral surface *
z = z ( x , y ) (( x , y ) )![]()
where σ is the projection of the surface S on the Oxy coordinate plane, z ( x , y ) is a single-valued continuously differentiable function, and the function f ( x , y , z ) is defined and continuous at each point of the surface S , then
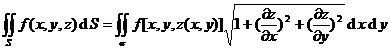
This integral is independent of the orientation of surface S (the direction of the normal) .
2 ° If the surface S is defined by a continuously differentiable function
 (( u , )
(( u , ) ![]() ∈ Ω )
∈ Ω )
given, then
![]()
in the formula
![]()
![]()
![]()
![]()
* The selection of the normal direction of a point on the surface uniquely determines the normal direction of all other points on the surface, they are the selected direction
The direction in which the normal moves continuously on the surface (without going through the edge of the surface), so it also determines the side of the surface . If you change the original selection
, the normal direction of all other points on the surface changes, and the surface moves from side to side . This surface is called
Double side surface .
[ Surface integration of coordinates ] If S is a smooth two-sided surface, it is its front side, that is, the side determined by the normal direction n (cos α , cos β , cos γ ) , P = P ( x , y ) , z ), Q = Q ( x , y , z ), R = R ( x , y , z ) are defined and continuous functions on the surface S , then![]()
![]()
If the surface S is defined by a continuously differentiable function
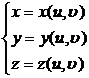 (( u , )
(( u , ) ![]() ∈ Ω )
∈ Ω )
given, then
![]()
in the formula
![]()
[ Stokes formula ] If C is a piecewise smooth simple closed curve surrounding a piecewise smooth and bounded two-sided surface S , P = P ( x , y , z ), Q = Q ( x , y , z ), R = R ( x , y , z ) is a continuously differentiable function on S + C , then
![]()
[ Gaussian formula ] If S is a piece-wise smooth surface containing volume V , P = P ( x , y , z ), Q = Q ( x , y , z ), R = R ( x , y , z ) and one of The first partial derivative is continuous on V + S , then there is a Gaussian formula:
![]()
where cos α , cos β , cos γ are the direction cosines of the positive direction of the normal of the surface S.
4.
Approximate calculation of double integral, curve integral and surface integral
[ Approximate formula for double integral ]
![]()
In the formula, different constants are selected for different integration regions Ω , which is the integration coefficient, and R is the remainder .![]()
![]()
Ω is circular C : ![]() ≤ A c = π
≤ A c = π![]()
![]()
|
n |
icon |
|
|
R |
|
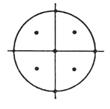
5 |
|
(0,0) ( ± h ,0) (0, ± h ) |
|
|
|
4 |
|
|
|
|
|
n |
icon |
|
|
R |
|
7 |
|
(0,0) ( ± h ,0)
|
|
|
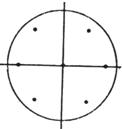
|
9 |
|
(0,0) ( ± h ,0) (0, ± h )
|
|
|
|
7 |
|
(0,0) ( ± h ,0) ( ± h , ± h ) |
|
|
|
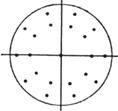
twenty one |
|
(0,0) (
(
k =1,2, … ,10 |
|
|
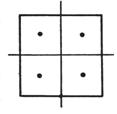
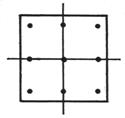
Ω is a square S : |x| ≤ h , | y | ≤ h , ![]() =4
=4![]()
|
n |
icon |
|
|
R |
|
9 |
|
(0,0) ( ± h , ± h ) ( ± h , 0 ) (0, ± h ) |
|
|
|
n |
icon |
|
|
R |
|
4 |
|
|
|
|
|
9 |
|
(0,0)
|
|
|
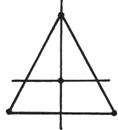
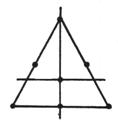
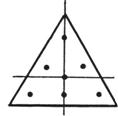
Ω is an equilateral triangle T : the radius of the circumcircle is h ,![]()
|
n |
icon |
|
|
R |
|
4 |
|
(0,0) ( h , 0 )
|
|
|
|
7 |
|
(0,0)
|
|
|
|
7 |
|
(0,0)
|
|
|
Ω is a regular hexagon H : the circumscribed radius is h ,![]()
|
n |
icon |
|
|
R |
|
7 |
|
(0,0)
( h , |
|
|
|
7 |
|
(0,0)
|
|
|
[ Approximate formula for triple integral ]
![]()
In the formula, different constants are selected for different integration regions V , which are the integration coefficients, and R is the remainder .![]()
![]()
V is a sphere S : ![]() ≤ . = π
≤ . = π![]()
![]()
![]()
![]()
|
n |
icon |
|
|
R |
|
7 |
|
(0,0,0)
|
|
|
V is a cube C : |x| ≤ h , | y | ≤ h, |z| ≤ h. =8
![]()
![]()
|
n |
icon |
|
|
R |
|
6 |
|
|
|
|
|
twenty one |
|
(0,0,0) 6 midpoints of the distance from the center to the 6 faces 6 -sided center 8 vertices |
|
|
|
n |
icon |
|
|
R |
|
42 |
|
6 -sided center midpoint of 12 edges 4 points on the diagonal of each face to the center of each face ( total 24:00 ) |
|
|
Ω is the tetrahedron T. is the volume of the tetrahedron![]()
|
n |
icon |
|
|
R |
|
8 11 |
|
4 vertices The center of gravity of the 4 faces center of gravity of T 4 vertices midpoint of 6 edges |
|
|
[ Approximate calculation formula of curve integral ]
|
|
Circumference : Curve integral over![]()
![]()
![]()
[ Approximate formula for surface integral ]
Sphere : Surface integral over![]()
![]()
![]()
|
n |
icon |
|
|
R |
|
6 |
|
|
|
|
|
n |
icon |
|
|
R |
|
18 |
|
|
|
|
|
26 |
|
|
|
|