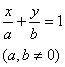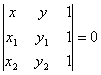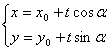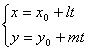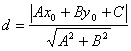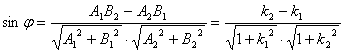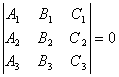§3 A straight line on a plane
1. Equations and graphs of a straight line in a plane
|
Equations and Graphics |
Description |
||||||
|
[ oblique cut ] |
|
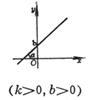
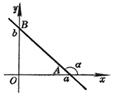
k is the slope . If the intersection angle between the line and the x -axis is a , then 0 £ a < p . b is the vertical intercept
|
|||||
|
|
|||||||
|
[ intercept ]
|
|
a , b are the intercepts on the x - axis and y -axis, respectively . The line passes through the points A ( a , 0) and B (0, b ) . Intersection angle with the x -axis
or |
|||||
|
[ dot slant ] |
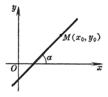
k is the slope The line passes through the point M ( x 0 , y 0 ) and intersects the x -axis at an angle
|
||||||
|
equation |
with graphics |
Description |
|||||
|
[ two-point type ]
or
|
|
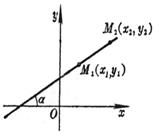
The straight line passes through two points M 1 ( x 1 , y 1 ) and M 2 ( x 2, y 2 ) , Intersection angle with the x -axis
|
|||||
|
[ General formula ]
|
|
slope Longitudinal intercept [ Note ] The general equation can be transformed into the above four forms as needed
|
|||||
|
[ parameter ]
or ( - ∞ < t < ∞ ) |
|
slope The straight line passes through the point M ( x 0 , y 0 ) and the intersection angle with the x -axis is a
|
|||||
|
[ Polar Coordinate Form ] |
|
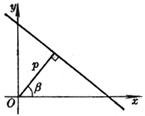
O is the pole, Ox is the polar axis, p is the distance from the pole to the line . a is the angle between the polar axis and the vertical line leading from the pole to the line ( positive counterclockwise ) , j is any point on the line Polar angle of M, r is the vector radius of point M
|
|||||
|
[ normal type ]
|
p is the length of the normal line ( the length of the vertical line from the origin O to the line ) , b is the intersection angle between the normal line and the x -axis, and p and b are called the position parameters of the line . [ Note ] The general formula of a straight line can be transformed into a normal formula In the formula, it is called the normalization factor of the straight line. When C < 0 ( or C = 0 and B > 0) , take the positive sign; when C > 0 ( or C = 0 and B < 0) , take the negative sign |
||||||
|
[ vector ]
|
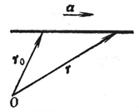
The line passes through the end point of the vector radius r 0 and is parallel to the known vector a
|
||||||
|
equation |
with graphics |
Description |
|||||
|
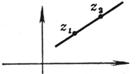
[ plural ]
( a )
( b )
|
|
(a) The line passes through the point z 0 and intersects the x -axis at an angle a
( b ) The straight line passes through two points z 1 , z 2 ( t is a real parameter ) |
|||||
The relationship between points and lines on a plane
|
Equations and Graphics |
Calculation formula and description |
|
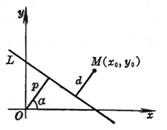
[ distance of dotted line ] normal general
|
d method =
where d is the distance from point M ( x 0 , y 0 ) to straight line L |
|
[ Included angle between two straight lines ] L 1 A 1 x + B 1 y + C 1 = 0 The slope is k 1 L 2 A 2 x + B 2 y + C 2 = 0 The slope is k 2
|
In particular, when ( or ) , L 1 // L 2 ; At that time , L 1 coincides with L 2 ; When A 1 A 2 + B 1 B 2 = 0 ( or 1 + k 1 k 2 = 0) , L 1 ⊥ L 2
|
|
Equations and Graphics |
Calculation formula and description |
|
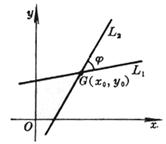
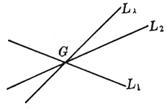
[ Conditions for straight line bundle × three straight lines co-point ] L l ( A 1 x + B 1 y + C 1 ) + l ( A 2 x + B 2 y + C 2 ) = 0, ( l is a parameter, - ¥ < l < ¥ )
|
For a certain value of l, L l represents a straight line passing through the intersection point G of two straight lines ( L 1 and L 2 ) . When l takes all values, the whole of the straight lines that L l represents passing through G is called a straight line bundle, G is called the vertex ( or center ) of the bundle of lines. Let L 3 be A 3 x + B 3 y + C 3 = 0 , then the condition for the three straight lines L 1 , L 2 , and L 3 to have the same point is the determinant If the equation of the two straight lines is given in the normal form, then | l | is the ratio of the distance between any point on the straight line L l and the two given straight lines, and the lines corresponding to l = 1 and l = - 1 are the given two straight lines Bisector of included angle
|