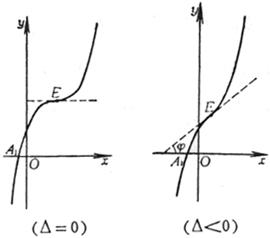
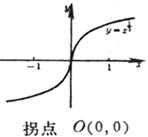
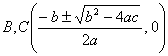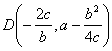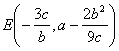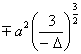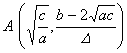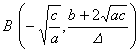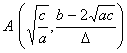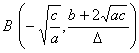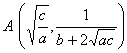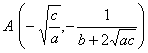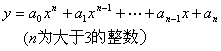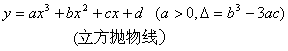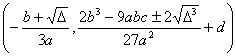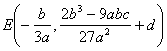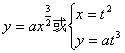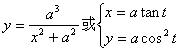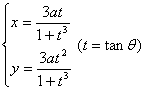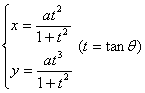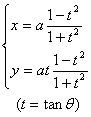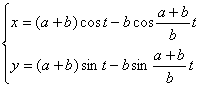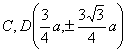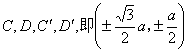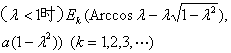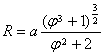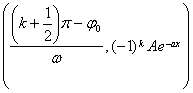§8 Important plane curve table
[ cubic curve ]
|
Equations and Graphics |
Features |
|
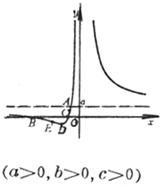
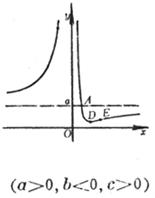
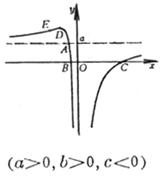
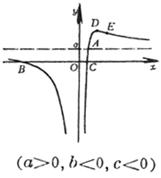
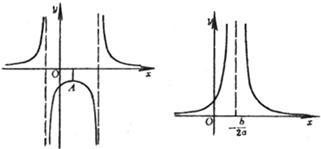
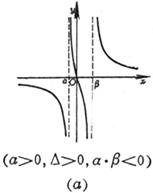
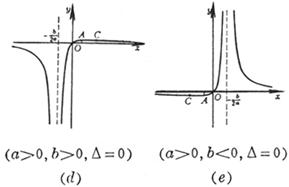
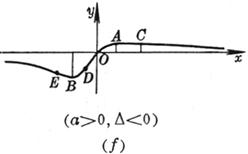
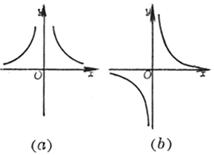
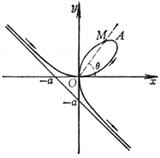
(a >0 , b<0 ,Δ>0) (a >0 , b<0 ,Δ=0) (a) (b) These curves are all symmetrical about a straight line |
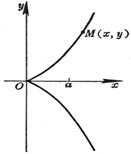
The curve consists of two Asymptote y = a and x = 0 The intersection of the curve with y = a The intersection of the curve and the x -axis Extreme point inflection point
( a ) discontinuity point maximum point asymptote _
（b） discontinuity point asymptote _ （c） maximum point inflection point The slopes at these two points are Asymptote y = 0
|
|
Equations and Graphics |
Features |
|
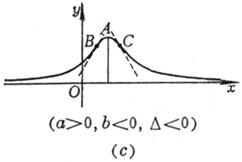
[ Note ] a , b are the two roots of the equation , and let
|
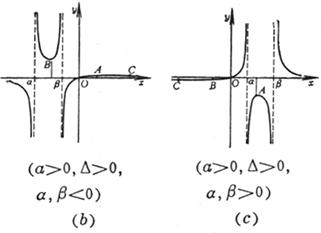
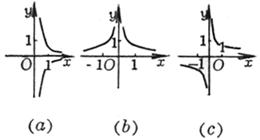
（a） Discontinuous point x = a , x = b Asymptote y = 0 and x = a , x = b （b） Discontinuous point x = a , x = b maximum point minimum point Inflection point C Asymptote y = 0 and x = a , x = b ( c ) Discontinuous point x = a , x = b maximum point minimum point Inflection point C Asymptote y = 0 and x = a , x = b （d） discontinuity point maximum point Inflection point C Asymptote y = 0 and （e） discontinuity point minimum point Inflection point C Asymptote y = 0 and （f） maximum point minimum point Inflection point C , D , E three points Asymptote y = 0 |
The graph of the above cubic curve only lists the cases where a > 0. For a < 0 , the division curve (when a > 0 , the asymptote is above the x -axis, and when a < 0 , the asymptote is below the x - axis) ), generally after making appropriate changes, the curves with a > 0 are symmetrical about the x -axis . For example , when a < 0 , the two curves: and are symmetrical about the x -axis, while the latter has a x 2 coefficient .
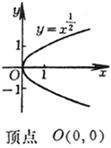
[ Parabolic Curve ]
|
Equations and Graphics |
Features |
|
|
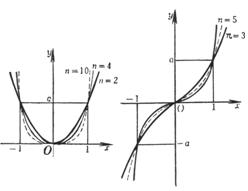
(a) , where n is even: y changes from to Odd number of extreme points ( 1 ~ n - 1 ) Even number of inflection points ( 0 ~ n - 2 )
(b)
, where n is odd y changes from to Even number of extreme points ( 0 ~ n - 1 ) Odd number of inflection points ( 1 ~ n - 2 )
The intersections A 1 , A 2 , A 3 ( or an intersection A 1 ) of the curve and the x -axis are the intersections of the real roots of the equation and the y -axis C ,
D at the extreme point ( C takes a positive sign, D takes a negative sign) inflection point it is a curve
the center of symmetry of , the slope of the tangent at this point is
|
|
Equations and Graphics |
Features |
|
(a) (b) |
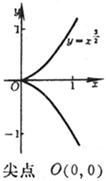
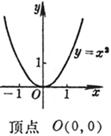
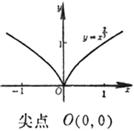
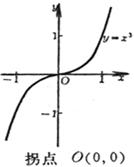
(a) , where n is even: Vertex (same extreme point) O (0, 0) The curve is symmetrical about the y -axis (b) , where n is odd: Inflection point O (0, 0) The curve is symmetrical about the origin
|
( m , n are two co-prime integers)
|
|
n is even m odd |
n is odd meven _ |
n is odd m odd |
Tangent case |
|
m>n
m<n
Symmetric case |
Symmetry about the x -axis |
Symmetry about the y -axis |
Symmetry about the origin |
Tangent to the x -axis at the origin
Tangent to the y -axis at the origin |
|
Equations and Graphics |
Features |
|
[ Hyperbolic Curve ]
[ Half-cubic parabola ] [ Kei tongue line ]
[ Cartesian lobe line ] or
[ vine leaf line ] or or [ ring rope ] or or
[ Nagomedus Clam Line ] or or (positive sign for outer branch, negative sign for inner branch)
|
( a ) n is even: Discontinuity point O ( 0, 0 ) Asymptote y = 0 and x = 0 The curve is symmetrical about the y -axis ( b ) n is odd: The curve is symmetrical about the origin
( a ) , where n is even and m is odd: Discontinuity point O ( 0, 0 ) Asymptote y = 0 and x = 0 The curve is symmetrical about x ( b ) , where n is odd and m is even: The curve is symmetric about y ( c ) , where n is odd and m is odd: The curve is symmetrical about the origin
The point at which the cusp is tangent to the x -axis Radius of curvature arc length
the maximum point at which the radius of curvature is The inflection point, the slopes of the tangent lines at these two points are asymptote _ area between curve and asymptote
The node at which it is tangent to the x and y axes and has a radius of curvature of vertex asymptote The area enclosed by the trap area between curve and asymptote
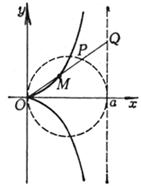
The curve is the locus of the point M made ( P is the intersection of the mother circle of diameter a and OQ ) The cusp at which the curve is tangent to the x - axis asymptote area between curve and asymptote
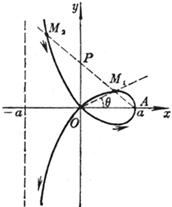
The curve is the locus of points M 1 , M 2 that make PM 1 = PM 2 = OP ( P is a point on the y -axis, M 1 , M 2 are on the ray passing through the two points A , P ) vertex A ( a , 0) Node O (0 , 0) Asymptote x = - a The area enclosed by the trap area between curve and asymptote
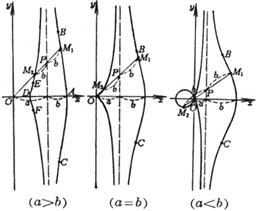
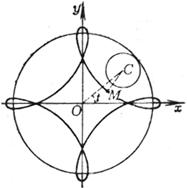
The curve is the locus of points M 1 , M 2 such that OM 1 = OP + b , OM 2 = OP - b ( referred to as outer branch ( right ) and inner branch ( left ), respectively) Outer branch Vertex A ( a + b , 0) Inflection points B , C whose abscissas are equal to the largest root of the equation x 3 – 3 a 2 x + 2 a ( a 2 – b 2 ) = 0 Inner branch Vertex D ( a - b , 0) Inflection points ( when a > b ) E , F , whose abscissas are equal to the second positive root of the equation x 3 – 3 a 2 x + 2 a ( a 2 – b 2 ) = 0 cusp ( when a = b ) O (0, 0) Node ( when a < b ) O (0, 0) Asymptotes of the inner and outer branches x = a |
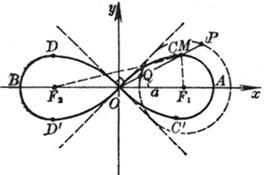
[ Pascal Snail ]
or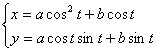 
or
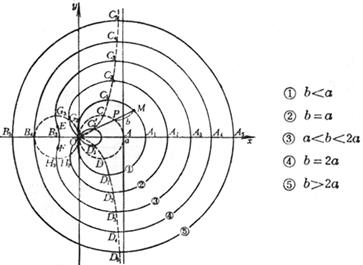
The curve is the locus of point M such that OM = OP ± b (point P is on a circle of diameter a )
Vertices A k , B k ( a ± b , 0)( k =1, 2, 3, 4, 5) , B 2 coincides with the origin
The node ( when b < a ) is O (0, 0) , the slope of the tangent at this point is , and the radius of curvature of this point is 
cusp ( when b = a ) O (0, 0)
Outliers ( when b > a ) O (0, 0)
There are 4 extreme points when b < a , and 2 when b 3 a : when b changes from 0 to ￥ , all extreme points form a vine-leaf line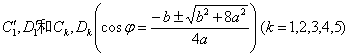 
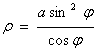
Inflection point ( when a < b < 2 a )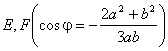
Tangent point of the double tangent ( when b < 2 a ):
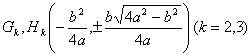
The area enclosed by these tangent points on the circle r = - a cos j by the snail line
(When b < a , the area of the inner circle is calculated twice)
[ Note ] When b = a , it is the heart line .
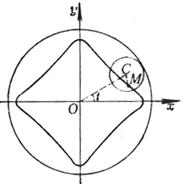
[ Cassini Oval Line ]
or
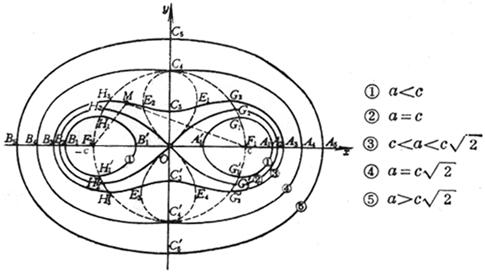
The curve is the locus of point M such that MF 1 × MF 2 = a 2 ( F 1 , F 2 are fixed focus, F 1 F 2 = 2 c , a is constant) .
vertex 
Extreme point 
or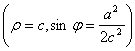
When a changes from 0 to 0 , all extreme points form a circle (radius c )
inflection point 
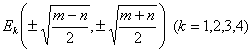
in
or
When a changes from c to , all inflection points form a double kinks
[ Note ] When a = c , it is a double dash .
|
[ heart line ]
or or
[ double twist ] or
[ Ordinary Trochoid (Cycloid) ]
or
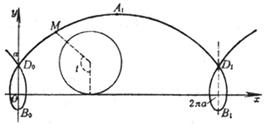
[ Long (or short) spoke trochoids (trochoids) ]
Long axis ( λ > 1)
Short axis ( λ < 1)
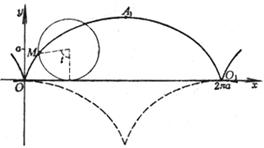
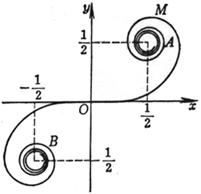
[ Hypotrochle (Epicycloid) ]
( a is the radius of the fixed circle, b is the radius of the moving circle, t = D COx )
|
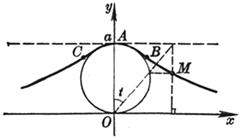
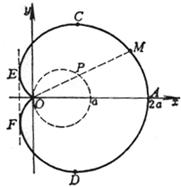
(i) It is the locus of point M such that OM = OP ± a ( a is the diameter of the circle, P is a point on the circumference) ( ii ) It is a special case of epitrochoid (moving and definite circles have equal diameters) cusp O (0 , 0) Vertex A (2 a , 0) Extreme point Tangent point of double tangent Curve length L = 8 a area
(i) It is the locus of point M such that MF 1 × MF 2 = a 2 ( OF 1 = a ) (ii)
It is the locus of point M such that OM = PQ ( P , Q on a circle with center F1 and radius ) Node (same as the inflection point ) O (0, 0) at which the slope of the tangent is ± 1 vertex Extreme point Radius of curvature Double knot area S = 2 a 2
The curve is the trajectory drawn by a point M on the circumference when a circle rolls along the x -axis without sliding (the radius of the circle is a ) Period T = 2 p a Extreme point Radius of curvature The involute is a cycloid (dotted line in the figure) arch length area
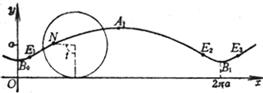
A curve is a track that a circle rolls along the x -axis without sliding pairs, a point M outside the circle (or a point N inside the circle ) (the radius of the circle is a ) Period T = 2 p a node _ inflection point maximum point minimum point Radius of curvature The radius of curvature corresponding to the extreme point ( when l < 1 ) is
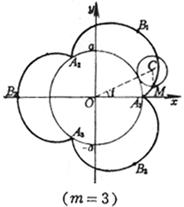
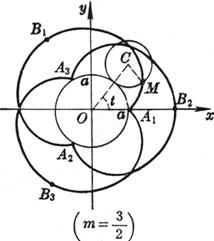
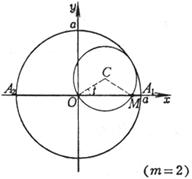
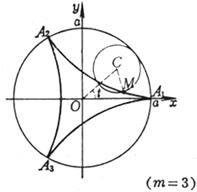
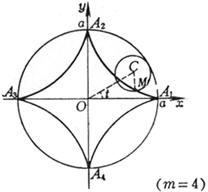
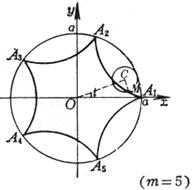
A curve is the trajectory drawn by a point M on the circumference when one circumference rolls along the outside of another circumference without sliding, and the shape of the curve is determined by the value of (i) When m = 1 , the curve is the heart line (ii) When m is an integer, the curve consists of m branches. After the moving point M traces the m branches (that is, the moving circle circles around the fixed circle), it returns to the starting position. (iii)
When m is a fraction ( , g , h are co-prime integers), the curve is composed of g branches. After the moving point M traces the g branch (that is, the moving circle revolves around the fixed circle h ), it returns to the starting position (iv) When m is an irrational number, there are infinitely many branches, and the moving point M cannot return to the starting position
sharp point
Vertex (where k is an integer, when m is an integer, ; then , ; when m is an irrational number, ) Curve length (one piece) Radius of curvature Area of sector A 1 B 1 A 2 A 1 (excluding the area of the fixed circle)
|
[ Hypotrochle (hypocycloid) ]
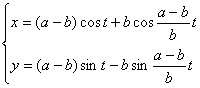
( a is the radius of the fixed circle, b is the radius of the moving circle, t = D COx )
A curve is the trajectory traced by a point M on a circle when one circle rolls along the interior of another circle without sliding .
The coordinates of the cusp, vertex, arc length, radius of curvature and area of the epitrochle are the same as those of the epitrochle, just replace " + b " with " -b " . It is always greater than 1 , especially , when m = 4 , there are 4 curves , called star-shaped lines, and the equation is
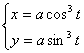or
Full curve length L = 6 a
The area enclosed by the curve 
[ Long (or short) spoke epitrochoids (exotrochoids) ]
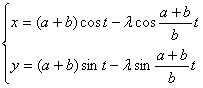( a is the radius of the fixed circle, b is the radius of the moving circle)
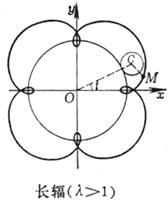
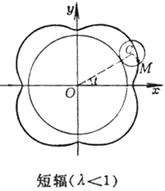
A curve is the trajectory traced by a point M outside ( or inside ) a circle when one circle rolls along the outside of another circle without sliding .
[ Long ( or short ) spoke hypotrochle (hypotrochoid) ]
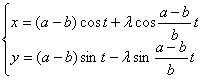( a is the radius of the fixed circle, b is the radius of the moving circle)
long spokes short spokes
A curve is the trajectory traced by a point M outside ( or inside ) a circle when one circle rolls along the inside of another circle without sliding . In particular, when a = 2 b , the long and short spoke hypotrochle is an ellipse; When a = b , it is a Pascal thread .
|
Equations and Graphics |
Features |
|
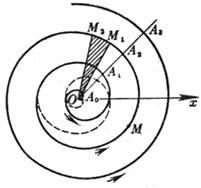
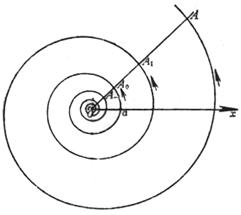
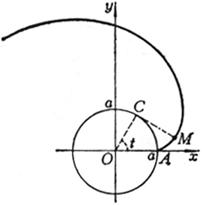
[ Archimedes Spiral ]
|
The curve is the trajectory drawn by a moving point when it moves along a ray at a constant speed , and the ray rotates around the pole O at a constant angular velocity . The curve consists of two curves, which are symmetrical about the x -axis . (in the equation , ) The ray and the curve passing through the pole are equally spaced at A 0 , A 1 , A 2 , L , and they are equally spaced ( ) arc length Radius of curvature Area of sector M 1 OM 2 |
|
[ Logarithmic spiral (equiangular spiral) ]
|
The angle of intersection of the curve and all rays passing through the pole is equal (a)(k=cota) , when the curve rotates clockwise around the pole and tends to the pole The ray and the curve passing through the pole in the proportionality intersect at L , A -1 , A 0 , A 1 , L , then L , , OA 0 , OA 1 , L , each line segment is a proportional series (common ratio is ) arc length Radius of curvature [ Note ] At that time , it was a circle |
[ Hybolic spiral ( inverse spiral )]
Asymptotic point pole O ( at that time ) 
Asymptote y = a
Radius of curvature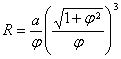 
Area of sector M 1 OM 2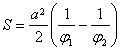 
The curve consists of two legs, which are symmetrical about the y -axis
[ Chain Helix ]
The curve is the locus of the point M that keeps the area of the circular sector OMN constant when N moves on the x -axis
Asymptotic point pole O ( at that time ) 
Asymptote x - axis ( at the time ) 
|
Equations and Graphics |
Features |
|
[ circular involute ] |
cusp A ( a ,,0) Intersection with the x -axis B ( ,0) (where t 0 is the root of the equation t = tan t ) arc length Radius of curvature The center of curvature C is on the circumference The curve consists of two legs, which are symmetrical about the x -axis |
|
[ clothoid ]
|
Inflection point O (0,0) Asymptotic point A ( ) B( ) arc length The curve is symmetrical about the origin |
|
Equations and Graphics |
Features |
|
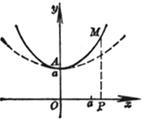
[ catenary ] |
vertex A (0, a ) arc length The area of the curved-sided trapezoid OAMP
Radius of curvature The curve is symmetrical about the y -axis and lies above the parabola y = a + (dashed line in the figure) [ Note ] Suspend a soft and inextensible heavy rope from the Two points, we get the shape of the catenary
|
|
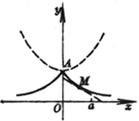
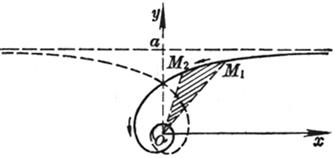
[ tracing line ] x=aArch or x=aln |
cusp A (0, a ) at which point is tangent to the y -axis arc length = a ln Radius of curvature R = a cot The curve is symmetrical about the y -axis, and it is the involute of the catenary, which starts from the vertex A , and the distance from the intersection of the tangent to the x -axis to the tangent is a constant . [ Note ] the length of a soft and inextensible rope One end is tied to a mass point M , and the other end P moves along the axis x , Then the point M is drawn into a tractor shape |
[ Rose line ]
|
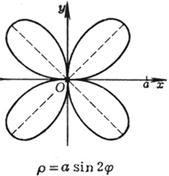
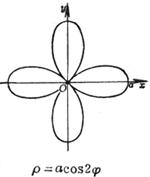
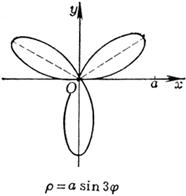
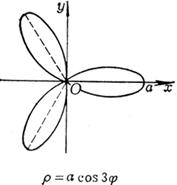
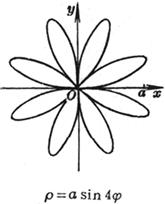
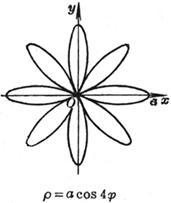
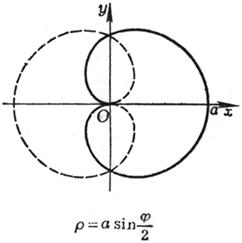
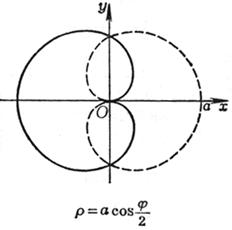
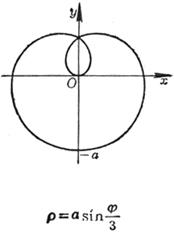
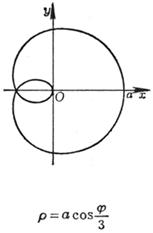
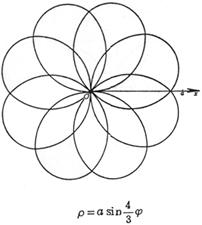
Equations and Graphics |
Features |
|
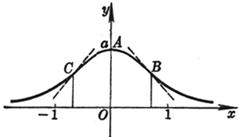
[ Probability Curve ] y=a
(a>0, k>0)
|
Vertex (Homomax) A (0, a ) Inflection point B , C The slope of the tangent at this point is The area between the curve and the x -axis The curve is symmetrical about the y -axis
|
|
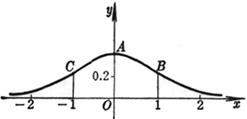
[ Standard normal distribution curve (Gaussian curve) ] y =
|
Vertex A (0, 0.3989) Inflection point B , C ( ) The area between the curve and the x -axis is 1 The curve is symmetrical about the y -axis |
|
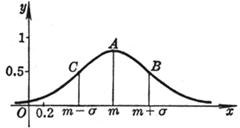
[ General normal distribution curve ] y =
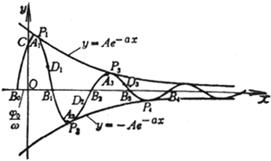
[ Damp vibration curve ] y=A
(A>0)
|
vertex (homomaximum point) A(m,) Inflection point B , C ( m ) The area between the curve and the x -axis is 1 The curve is symmetrical about the line x = m
Intersection with the x -axis Bk (k=1,2L) Intersection with y -axis C (0, A sin 0 ) The abscissa of the extreme point Ak is The abscissa of the inflection point Dk is Curve and Two Exponential Curves y = tangent, tangent point Pk |
