§ 9 Space Curve
1.
Basic concepts and formulas of curves
[ Equation and Forward of the Curve ]
|
The form of the curve equation |
Forward of the curve |
|
face to face parametric or ( t is an arbitrary parameter, s is the arc length of the curve) Vector r = r ( t ) or r = r ( s ) ( r ( t ) = x ( t ) i + y ( t ) j + z ( t ) k , t , s as above) |
The direction of movement of a point on the curve as t (or s ) increases |
|
Figure 7.18 |
[ Three unit vectors of the active frame ] t is the unit tangent vector, the direction is consistent with the positive direction of the curve; n is the unit principal normal vector, which points to the concave side of the curve; b is the unit secondary normal vector, b = t n . t , n , b form a right-handed system (Fig. 7.18 ) . These three vectors are called the movable frame of the curve at point M (or called the moving scalar trihedron, the adjoint trihedron, also called the movable scalar) .![]()
[ Equations of the line and plane where the movable frame is located ] Let M be ( x 0 , y 0 , z 0 ) (Figure 7.18 ) .
The 1° tangent line passes through two points N , M on the curve NM , the limit position when N M . Its equation is ![]()
Parametric formula (with t as a parameter)![]()
In the formula, it represents the value at the point M ( x 0 , y 0 , z 0 ) , etc. The parameter t can be taken as the arc length s , which is represented by , and so on .![]()
![]()
![]()
![]()
Vector formula r = r 0 + (with t as parameter) ![]()
where represents the value at point M ( x 0 , y 0 , z 0 ) , which is another parameter .![]()
![]()
![]()
face to face

where represents the value at point M , and so on .![]()
![]()
2° The plane where the normal surface is perpendicular to the tangent line ( all straight lines passing through the normal surface of M are called the normal line of the curve in M ) . Its equation is
Parametric formula ( x - x 0 )+ ( y - y 0 )+ ( z - z 0 )=0 (with t as a parameter) ![]()
![]()
![]()
In the formula, the arc length s can also be taken as a parameter .
Vector
( r - r 0 ) = 0 ![]() (with t as parameter)
(with t as parameter)
face to face

The 3° close plane passes through the three points M , P , N on the curve to make a plane. At that time , the limit position of the plane (the tangent line is on the close plane) . Its equation is ![]()
Parametric formula (with t as a parameter)

where represents the value at point M , etc., the parameter t can also be taken as the arc length s .![]()
![]()
Vector (( r - r 0 ) )=0 (with t as a parameter)![]()
The intersection of the 4° principal normal normal and the close surface . Its equation is
Parametric formula (with t as a parameter) 
in the formula
l = , m = , n =


![]() (with s as parameter)
(with s as parameter)
![]() represents the value at point M , etc.
represents the value at point M , etc.![]()
Vector formula r = r 0 + (with t as parameter)
![]()
r = r 0 +![]() (with s as parameter)
(with s as parameter)
where is another parameter .![]()
A line whose 5° binormal is perpendicular to the osculating surface . Its equation is
Parametric
![]() (with t as parameter)
(with t as parameter)
In the formula, l , m , and n are defined as formula (1) .
vector
r 0 = r 0 +![]() (with t as parameter)
(with t as parameter)
6° from the tangent plane through the tangent and binormal plane . Its equation is
Parametric formula (with t as a parameter) 
![]() (with s as parameter)
(with s as parameter)
vector
![]() (with t as parameter)
(with t as parameter)
![]() (with s as parameter)
(with s as parameter)
[ Definition and formula of curvature and torsion ]
|
formula and meaning |
graphics |
|
curvature
Radius of curvature
k represents the degree to which the partial curve including the point M deviates from the straight line, and is also the rotation rate of the tangential direction to the arc length |
|
|
torsion
torsion radius
The sign of the torsion rate : when the point M moves along the positive direction of the curve, the vector is opposite to n , then the positive sign is taken, otherwise, the negative sign is taken (Figure ( b ) ) |
( a )
( b ) |
The table represents the derivatives of t and b with respect to s , respectively .![]()
[ Calculation formula of curvature and torsion ]
1° curvature
Parametric
k = (with t as parameter)
k = (with s as parameter)![]()
vector
k =  or (with t as parameter)
or (with t as parameter)![]()
k = (with s as parameter)![]()
Absolute value of 2° deflection
Parametric
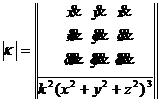 (with t as parameter)
(with t as parameter)
 (with s as parameter)
(with s as parameter)
vector
 or (with t as parameter)
or (with t as parameter)
![]() (with s as parameter)
(with s as parameter)
In the formula, s is the arc length, t is an arbitrary parameter, " ¢ " means derivation with respect to s , and " × " means derivation with respect to t .
[ Sherley - Fleiner formula (or basic formula) ]
![]() , ,
, ,![]()
![]()
In the formula, t , n , b are the three basic unit vectors of the movable frame, which are the radius of curvature and the radius of torsion . The feature of this group of formulas is that the derivatives of the basic vectors t , n , b with respect to the arc length s can be used t , It is expressed as a linear combination of n , b , and its coefficients form an antisymmetric square matrix:![]()
![]()

This set of formulas combined with = t describe the motion law of the movable frame when the point M moves on the curve .![]()
The movable frame is regarded as a rigid body, that is, when M moves along the curve, the movable frame of M rotates around M like a rigid body . At this time, s is regarded as time, and the movable frame can be obtained according to the principle of kinematics The expression for the instantaneous rotational speed of
![]()
This shows that the rotation vector falls on the normal plane . This instantaneous rotation vector is called the Darb's vector . It is only decomposed into two vectors t and b , so the instantaneous rotation of the movable frame can be regarded as the sum of the two rotations . A rotation Corresponding to t , according to the definition of rotational speed, it rotates around the axis whose direction is t ; the other rotates around the axis whose direction is b . Therefore, the kinematic meaning of curvature and torsion is obtained:![]()
![]()
![]()
![]()
![]()
The curvature of the curve is equal to the rotation of the movable frame around the secondary normal, and the torsion is equal to the rotation around the tangent .
Finally, it can be verified that the Shelley - Fleiner formula for the space curve is![]()

This is the kinematic meaning of the Shelley - Fleiner formula .
[ Basic Theorem and Natural Equation ] Given any two continuous functions k ( s ) and ( s ) on a closed interval a s b , where k ( s )>0 , except for the position difference in space, there is a unique A curve in space with s as the arc length, with k ( s ) as the curvature and ( s ) as the torsion .![]()
![]()
![]()
![]()
equation set
k = k ( s ), = ( s )![]()
![]()
Natural equations called space curves .
2.
Equations and graphs of the spiral
[ General helix ] A space curve whose intersecting angle with the cylindrical generatrix is a fixed angle ( ) is called a general helix (or a curve of fixed inclination) . This curve has the properties:![]()
The ratio of 1° curvature to torsion is equal to a constant ( k = tan ).![]()
![]()
The intersection angle between the 2° tangent and a fixed direction is a fixed angle ( ).![]()
The 3° principal normal is perpendicular to a fixed direction .
The intersection angle between the 4° secondary normal and a fixed direction is a fixed angle .![]()
|
Figure 7.19 |
[ Cylinder helix ] A moving point rotates at a constant speed around a line and moves at a constant speed along the line, then the trajectory of this moving point is called a cylindrical helix (Figure 7.19 ), and its parameter equation is

In the formula , is the angular velocity, h is called the pitch, and is called the helix angle. In the formula, the positive sign is taken for the right helix and the negative sign for the left helix. If the arc length s is used as the parameter, the equation is:![]()
![]()
![]()
|
Figure 7.20 |

Both curvature and torsion are constants: k = ,![]()
![]()
A curve whose intersecting angle with a conical surface generatrix is a fixed angle is called a conic helix (Fig. 7.20 ) , and its equation is

In the formula, it is half of the cone apex angle, which is the helix angle, which are all constants . Since this curve is projected on the Oxy plane as a logarithmic spiral, it is also called a cone logarithmic spiral .![]()
![]()
![]()







