§ 3    Affine Coordinate System

 

1. Affine coordinate system and metric coefficients

 

    [ Affine coordinates ]   In the three-dimensional Euclidean space V , if a rectangular coordinate system is taken, and its coordinate unit vectors are i , j , and k , the vector a in the space can be expressed as

a = a _x i + a _y   j + a _z k

    Generally, given three non-coplanar vectors e ₁ , e ₂ , e ₃ in the space, any vector a in the space can be decomposed according to these three vectors, and let its coefficients be a ¹ , a ² , a ³ ( here 1 , 2, 3 are not exponents, but superscripts ) , then a can be expressed as

a = a ¹ e ₁ + a ² e ₂ + a ³ e ₃

Or simply count as V V a = a ⁱ e _i                      

a = a ¹ , a ² , a ³ ={ a ⁱ } V V V

Such coordinate systems e ₁ , e ₂ , e ₃ are called affine coordinate systems, e ₁ , e ₂ , e ₃ are called coordinate vectors, and a ¹ , a ² , a ³ are called affine coordinates of vector a .

    [ Metric coefficient in Euclidean space ]   When the vector a is written in the above form, its length a is given by

( a ) ² = ( a ⁱ e _i )( a ^j e _j ) = ( e _i e _j ) a ⁱ a ^j

give . order

e _i e _j = g _ij (= g _ji )   ( i , j =1,2,3)

Then gij is called the metric coefficient of the _affine coordinate system .

    1 The length of the vector a is given by 

( a ) ² = g _ij a ⁱ a ^j

Calculate .

    2   two vectors

a = a ⁱ e _i , b = b ^j e _j

The included angle is given by

cos =

Calculate .

    3   Since g _ij a ⁱ a ^j is a positive definite quadratic form, the determinant made by g _ij

mixed product

( e ₁ , e ₂ , e ₃ ) ² = = g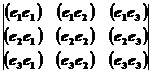

( e ₁ , e ₂ , e ₃ )=

    [ Kronecker notation ]   Symmetric matrix

The inverse matrix of

to represent . By the properties of the inverse matrix, there are g ^ij = g ^ji and

g ^ik g _kj =

in the formula

=

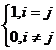
called Kronecker notation .

    [ reciprocal vector ]   use this g ^ij provision

e ⁱ = g ^ij e _j

Hence there is

e _j = g _ij e ⁱ

e ⁱ e _k =( g ^ij e _j ) e _k = g ^ij ( e _j e _k )= g ^ij g _jk =

e ⁱ e ^j =( g ^il e _l )( g ^jm e _m )= g ^il g ^jm ( e _l e _m )= g ^il g ^jm g _lm = g ^il = g ^ij

    For e ₁ , e ₂ , e ₃ , we can get

e ¹ =( e ₂ × e ₃ ),

e ² =( e ₃ × e ₁ ), e ³ =( e ₁ × e ₂ )

e ¹ , e ² , e ³ are called reciprocal vectorsabout the coordinate vectors e ₁ , e ₂ , e _3. g ^ij is called the metric coefficient inthe affine coordinate system of the reciprocal vectors.

 

Two, contravariant vector and covariant vector

 

    [ Contravariant vector and covariant vector ]   If the affine coordinates a ¹ , a ² , a ^{3 of the vector} a in the coordinate systems e ₁ , e ₂ , e ₃ are determined by the formula

a = a ¹ e ₁ + a ² e ₂ + a ³ e ₃ = a ⁱ e _i

Given, a ¹ , a ² , a ³ are called contravariant coordinates ( or called anti-variation coordinates ) of vector a , and vector a ⁱ is called a contravariant vector ( or called anti-variation vector ).

    If the reciprocal vectors about the coordinate vectors e ₁ , e ₂ , e _{3 are} e ¹ , e ² , e ³ , the affine coordinates a ₁ , a ₂ of the vector a in the coordinate systems e ¹ , e ² , e ³ , a3 is determined by the _formula

a = a ₁ e ¹ + a ₂ e ² + a ₃ e ³ = a _j e ^j

given, then a ₁ , a ₂ , a ₃ are called covariant coordinates of vector a, and vector a j is _called covariant vector .

    In the Cartesian coordinate system, the covariant coordinates and contravariant coordinates of the vector are consistent . Generally, in the affine coordinate system, the covariant coordinates and the contravariant coordinates have a relationship

a _i = a · e _i =( a ^j e _j ) · e _i = a ^j ( e _j · e _i )= a ^j g _ji

[ scalar product of contravariant vector and covariant vector ]

    If a , b are two vectors, a ¹ , a ² , a ³ ; b ¹ , b ² , b ³ are their contravariant coordinates, respectively, then

a · b = g _ij a ⁱ b ^j

    If a , b are two vectors, a ¹ , a ² , a ³ ; b ₁ , b ₂ , b ₃ are their covariant coordinates, respectively, then

a · b = g ^ij a _i a _j

If the contravariant coordinates of a are a ¹ , a ² , a ³ , and the covariant coordinates of b are b ¹ , b ² , b ³ , then

a · b = a ⁱ b _i

 

Three, n -dimensional space

 

    [ Definition of n -dimensional space ]   If a point in the space has a one-to-one correspondence with the values ​​of an ordered group of n independent real numbers x ¹ , ···, x ⁿ , then, take such a point as an element The set of is called n -dimensional real number space V ( referred to as n -dimensional space ) , denoted as R ⁿ . So a point M in the space corresponds to a set of ordered numbers x ¹ ,..., x ⁿ ; on the contrary, a set of ordered numbers x ¹ , ···, x ⁿ corresponds to a point M. Such a set of ordered numbers ( x 1 ^, ···, x ⁿ ) is called an n -dimensional spaceThe coordinates of a point M in R ⁿ .

    [ Vector in n -dimensional space ]   Take a certain point O in the n -dimensional space R ⁿ with coordinates (0,0, ··· ,0) , and another point M ( x ¹ , x ² , ···, x ⁿ ) , r is a vector corresponding to two points O and M , called the vector radius of point M.

    It is assumed that an affine coordinate system can be introduced in R ^{n such that the relationship between the vector radius} r and the coordinates of the point M ( x ⁱ ) is

r = x ¹ e ₁ +... + x ⁿ e _n = x ⁱ e _i

where e ₁ , ···, e _n are n linearly independent vectors in R ⁿ , and this coordinate system e _{1 ,} ··· , e _{n is} called an affine coordinate system in R ⁿ , x ¹ , · , x ^{n is} called the affine coordinate of the vector r in R ⁿ .

    Many of the results discussed in the three-dimensional space are valid in the n -dimensional space, as long as the indicators appearing in the formula are considered to be from 1 to n .

    [ Contravariant vector and covariant vector ]   Consider an arbitrary coordinate transformation in the n -dimensional space R ⁿ

V V (1)                         

where the function has successive derivatives with respect to x ⁱ ( the order required in the discussion ) , and the Jacobian of the transformation is not equal to zero:

Therefore (1) has an inverse transform

    Let a ¹ , ··· , a ⁿ be the function of x ⁱ , if under the coordinate transformation, they are all transformed according to the coordinate differential, that is

Then a ⁱ is called the contravariant coordinate of a vector in the coordinate system ( x ⁱ ) , and it is the contravariant coordinate of the same vector in the coordinate system . The vector is called the contravariant vector .

    If a _i press

form transformation, then a ⁱ is called the covariant coordinate of a vector in the coordinate system ( x ⁱ ) , and it is called the covariant coordinate of the same vector in the coordinate system, and the vector is called the covariant vector .

    The transformation coefficients of contravariant and covariant vectors are different, but there is a relation between them

where is the Kronecker notation .

    The gradient of a scalar field is a covariant vector . 

    Let the scalar field in n -dimensional space be , its change along an infinitesimal displacement d x ⁱ

is an invariant under the coordinate transformation, where is the component of the gradient . Therefore, under the coordinate transformation,

but

So it is a covariant vector .