§ 5    Preliminary Riemannian geometry

 

1. Riemann space

 

[ Riemann space and its metric tensor ]  If there is a set of functions g _ij ( x ⁱ )= g _ji ( x ⁱ ) in the n -dimensional space R ⁿ , such that two adjacent points x ⁱ ,

The distance ds between x ⁱ + d x ⁱ is given by a positive definite quadratic form

d s ² = g _ij ( x )d x ⁱ d x ^j

Determined, then the space R ⁿ is called Riemann space, denoted as V ⁿ . The geometry in the Riemann space V ⁿ is called Riemann geometry . The quadratic type ds ² is called the line element of V ⁿ . Differentiate into

And the arc length of any curve xi = ^{xi (} t ) is the integral

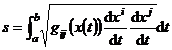
    because of the coordinate transformation

Next, ds ² is an invariant, so

This shows that g _ij ( x ) is a component of a second-order covariance tensor, which is called the metric tensor or fundamental tensor of the Riemann space V ⁿ .

    [ Length of vector, scalar product and angle of two vectors, adjoint tensor ] The definitions    of scalar ( field ) , vector ( field ) , tensor ( field ) , etc. in Riemann space are similar to the previous sections, and their operations The rules are also similar .

    Let it be a contravariant vector, then the square of its length is

g _ij a ⁱ a ^j

    If and are two contravariant vectors, their scalar product is

g _ij a ⁱ b ^j

The cosine of the angle between the two vectors is

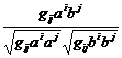
    Assume

g _ij a ⁱ = a _j , g _ij b ⁱ = b _j

Then and are covariant vectors, their length and scalar product are respectively

g _ij a ⁱ a ^j = a _j a ^j , g _ij a ⁱ b ^j = a _j b ^j

    The adjoint tensor of the tensor is

,

where g ^lj satisfies the equation

where is the Kronecker notation .

    [ Riemann contact and Christopher symbol ]  In Riemann space, the contact can always be determined in a unique way , satisfying the conditions:

    (i)   Affine connections are torsion-free, i.e.

    (ii) The parallel movement generated by the affine connection keeps the length of the vector constant . 

    This is called the Riemann connection or the Levy-Civita connection .

    According to the above two conditions, it can be obtained that

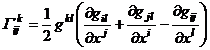
If you remember

then there are

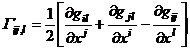
Sometimes the following notation is used:

and

They are called Christopher's three-index symbols of the first and second types, respectively .

    In addition, there is the equation

or

It should also be pointed out that all the results in § 4 concerning the covariant differential method hold for the Riemann connection .

 

2. The parallelism of Levi-Civita

 

    The parallel movement in the affine connection space is determined by the affine connection . In the Riemann space V ⁿ with the metric tensor g _ij , the Riemann connection ^is used to define the corresponding parallel movement called the Levy- Civita parallel movement .

    Suppose a vector field a ⁱ = a ⁱ ( t ) is given along a certain curve x ⁱ = x ⁱ ( t ) in V ⁿ , if an infinitesimal displacement is made along this curve, the vector a ⁱ ( t ) follows the law

change, then the vector a ⁱ ( t ) is said to perform a Levi-Civita parallel translation along the curve .

    The Levi-Civita parallel motion has the properties:

    1 The covariant derivative of the metric tensor g _{ij is equal to zero, i.e.} 

Also ,                            

    2   If the two families of vectors a ⁱ ( t ) and b ⁱ ( t ) move parallel to the curve, then

Therefore, the scalar product of the two vectors and the included angle remain unchanged under parallel translation .

    3   The self-parallel curves ( also called geodesics ) in the Riemann space V ⁿ are exactly the same as the self-parallel curves in the affine connection space, both of which are determined by the differential equation

But here is the Riemann connection . So a necessary and sufficient condition for a curve to be a geodesic is that its unit tangent vectors are parallel to each other .

 

3. Curvature in Riemann space

 

[ Curvature tensor and Lich's formula ]  The obvious difference between the covariant derivative of a tensor and the ordinary derivative is that when a higher-order derivative is obtained, the result of the tensor derivative is generally related to the order of the derivative . For example, when an operation acts on a vector , then there are         

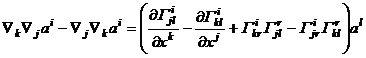                (1)

remember

It is a third-order covariant and first-order contravariant fourth-order mixed tensor, called the curvature tensor or Riemann-Christopher tensor of space V ⁿ .

The left side is called the staggered second-order covariant derivative of the contravariant vector ; the staggered second-order covariant derivative with respect to the covariant vector is

The interleaved second-order covariant derivative of a tensor is

This is called the Leach formula .

    [ Riemann notation · Lich tensor · Curvature scalar · Einstein space ]

    covariate component of curvature tensor

are called Riemann symbols of the first kind, and Riemann symbols of the second kind .

    The curvature tensor shrinks to get

is called the Ricci tensor . The Ricci tensor is then contracted to get

R = g ^kl R _kl

called the curvature scalar .

    If the Leach tensor satisfies

This space is called Einstein space .

    [ Properties of Curvature Tensors ]

    1 The first two indices j and k of the curvature tensor are antisymmetric, i.e. 

very       

    2  The curvature tensor performs cyclic permutation of the three covariant indicators and adds them, so that

This is called the Lich identity .

    3   The first kind of Riemann symbol R _kjlr can be calculated as follows:

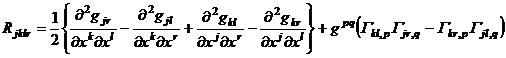
    Therefore , R _kjlr is antisymmetric with respect to indexes j , k and l , r; it is symmetric with respect to the former pair of indexes and the latter pair of indexes; after cyclic permutation of the first three indexes, the sum is equal to zero, that is,

R _jklr = - R _kjlr

R _jklr = -R _jkrl _

R _jklr = R _lrjk

R _jklr + R _kljr + R _ljkr = 0

4 The Lich tensor is symmetric, that is, R _kl = R _lk .  

    At any point in the 5  space V ⁿ , the following formula holds:

This is called the Pianchi identity . It states that the sum obtained by cyclic permutation of the index ( i ) of the covariant derivative and the first two indices ( j , k ) of the curvature tensor is equal to zero .

    [ Riemann curvature ( section curvature ) and constant curvature space ] do the  sum of two linearly independent vectors at a point M in the Riemann space V ⁿ

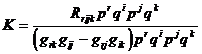
This is called the Riemannian curvature of the plane determined by p ⁱ , q ⁱ , also known as the section curvature .

    If for all points in space V ⁿ ( n > 2) we have

R _rijk = K ( g _rk g _ij − g _rj g _ik )

Then the Riemann curvature K is a constant, which is Schur 's theorem .

    A space V ⁿ with a constant Riemann curvature is called a space of constant curvature, and the line elements of this space can be transformed into the form

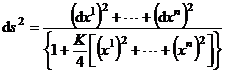
This is called a measure of a space of constant curvature in Riemann form .

    A space with constant curvature is an Einstein space .