§ 4 Unitary space
1. Definition and properties of unitary space
[ Unitary space and Euclidean space ] Let V be a linear space on the complex number field F , if the inner product (quantity product) of two vectors is defined in V , denoted as ( ), and satisfy:![]()
![]()
(i) ( ) = ( ), where ( ) is the complex conjugate of ( );![]()
![]()
![]()
![]()
(ii) ( ) , the equal sign holds if and only then ;![]()
![]()
![]()
(iii) ![]() , for any establishment;
, for any establishment;![]()
![]()
Then V is called a unitary ( U ) space, also known as an inner product space .
If F is the field of real numbers, then the inner product is commutative . The finite-dimensional real unitary space is called Euclidean space .
For example, in an n -dimensional linear space , if specified ![]()
![]()
in the formula
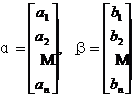
is a unitary space .![]()
The inner product in the unitary space V has the property:
1 o ( ) =![]()
![]()
2o _ ![]()
3 o general, then![]()
![]()
![]()
4o _ ![]()
[ modulus ( norm )] is real because of . Let![]()
![]()
![]()
Call it the modulus or norm of a vector in the unitary space V. A vector whose modulus is 1 is called a unit vector or a standard vector .![]()
Let α and β be vectors in unitary space, and c be a complex number, then
1 o![]()
2 o![]() (Cauchy - Schwartz inequality)
(Cauchy - Schwartz inequality)
The equal sign holds if and only if α and β are linearly related .
3o _![]()
These properties are independent of the dimensionality of the space .
[ Orthogonal and Standard Orthogonal Basis ] In the unitary space V , if , the vector α is said to be orthogonal to β . Obviously, if α is orthogonal to β , then β is also orthogonal to α .![]()
In unitary space, any set of two orthogonal nonzero vectors is linearly independent .
If a set of unit vectors is orthogonal to each other, it is called a standard orthogonal set . If this vector set generates the entire space V , it is called the standard orthonormal basis of
V.
Let { } be ![]() a set of standard orthonormal vectors in the unitary space V , , then
a set of standard orthonormal vectors in the unitary space V , , then![]()
1 o![]() (Bessel's inequality)
(Bessel's inequality)
2 o![]() is orthogonal to
is orthogonal to![]()
3 o When V is a finite-dimensional space, the necessary and sufficient condition for { } ![]() to be the basis of V is: any vector can be expressed as
to be the basis of V is: any vector can be expressed as![]()
![]()
![]()
and ![]()
[ Orthogonal Complementary Space of Subspace ] Let V be a unitary space on the complex field, and S be a subspace of V , if
(i)![]()
(ii) T is called the orthogonal complement space of S for the pair and there .![]()
![]()
![]()
It is immediately known from (i) (the empty set) .![]()
If S is a subspace of a finite-dimensional unitary space , then there is a subspace T that
is the orthogonal complement of S.![]()
![]()
2. Special linear transformation on unitary space
[ Conjugate transformation ] For a linear transformation L on the unitary space V on the field F , the transformation defined by the relational expression is a linear transformation , which is called the conjugate transformation of L. If , then L is called a normal transformation .
![]()
![]()
![]()
![]()
Conjugate transformations have the following properties:
1 o![]()
2o _![]()
3o _![]()
4o _![]()
5 o If L is a non-singular linear transformation, then it is also a non-singular linear transformation, and![]()
![]()
6 o If the matrix of L is A under a certain standard orthonormal basis , then the matrix of conjugate transformation about the same basis is the conjugate transpose matrix of A.![]()
![]()
[ Self-conjugate transformation (Hermitian transformation) ] If , then L is called self-conjugate transformation or Hermitian transformation .![]()
The self-conjugate transformation has the following properties:
1 oIf L and M are self-conjugate transformations, they are also self-conjugate transformations .
When L and M are commutative, LM is also self-conjugate transformation .
![]()
![]()
2 o Under the standard orthonormal basis, the matrix of self-conjugate transformation is Hermitian matrix . On the contrary, if the matrix of linear transformation about a standard orthonormal basis is Hermitian matrix, it must be self-conjugate transformation .
3 o The eigenvalues of the autoconjugate transform are real .
4 o There are suitable standard orthonormal bases such that the self-conjugate transformation L corresponds to a real diagonal matrix whose elements on the main diagonal are all the eigenvalues of L.
[ Unitary transformation ] If there is a linear transformation L for any in the unitary space V , then L is called a unitary transformation .![]()
![]()
The unitary transformation has the following properties:
1 o The identity transformation is a unitary transformation .
2 o If L and M are unitary transformations, then LM is also unitary transformations .
3 o If L is a unitary transformation, it is also a unitary transformation .![]()
The necessary and sufficient conditions for 4 o L to be a unitary transformation are:
![]() or
or ![]()
5 o Under the standard orthonormal basis, the matrix of the unitary transformation L is a unitary matrix .
On the contrary, if the matrix of the linear transformation about a standard orthonormal basis is a unitary matrix, it must be a unitary transformation .
The absolute values of the eigenvalues of the 6o unitary transformation are all 1 .
3. Projection
[ Projection and its properties ] For a linear transformation P on a linear space V , if there are two complementary subspaces S and T of V such that if , then![]()
![]()
This transformation P is called the projection of V on S along T.
Projection has the following properties:
1 o If P is a projective, then
![]()
Therefore, projection is an idempotent transformation; conversely, an idempotent transformation must be projective .
2 o If the linear space V is projective along and along respectively , then![]()
![]()
![]()
![]()
![]()
(i) is a projective if and only if if , then , and is a projective along the above .![]()
![]()
![]()
![]()
![]()
![]()
(ii) If , then P is a projective along .![]()
![]()
![]()
3 o Let T and S be two complementary subspaces of a finite-dimensional linear space , and P be the projection along subspace T on subspace S , then the matrix of P can be transformed into the following form:![]()
![]()
where A is a square matrix of order k .
[ Orthoprojection ] Let S and T be the complementary subspace of the unitary space V on the complex field, then the projection of V on S along T is called the orthoprojection of V on S.
[ Decomposition of self-conjugate transformation ] Let L be a self-conjugate transformation on a finite -dimensional unitary space V. Let be the different eigenvalues of L , and let be the set of vectors α that make , then it is the subspace of V. Obviously , and is the orthonormal complement space of V. If { } is an orthonormal basis of Si , where is the dimension of , then the set { } composed of all these is a canonical basis of V. Finally , let P i is the projection of V on Si , then with respect to the base above, L![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() The matrix has the following form:
The matrix has the following form:
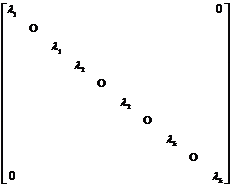 =
=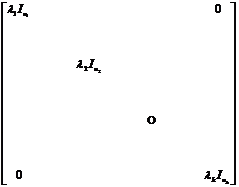
where represents the order identity matrix . On the other hand, the matrix about this basis projection P i is![]()
![]()

where represents a zero matrix of order .![]()
![]()
Therefore, the self-conjugate transformation can be written as a linear combination of projections .
![]()
4. Metrics in unitary space
In the first paragraph of this section, the modulus (norm) of each vector α in the unitary space has been introduced . The distance between two "points" (ie vectors) α, β in the unitary space and any two vectors α , β The angle is defined as follows:![]()
![]()
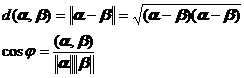
The function defined by the above equation satisfies all conditions in the scale space (see Chapter 21, § 4 , a) .
If V is a real unitary space, then for everything , the angle must be real .![]()
![]()