§ 6 Rowdang canonical form of square matrix
1. Invariant subspace
Let L be a linear transformation of a real (or complex) linear space V , and S be a subspace of V, if , then S is an invariant subspace about L.![]()
Let be an invariant subspace of a linear transformation L of an n -dimensional linear space V , and V can use their direct sum:![]()
![]()
The necessary and sufficient condition to represent is: the matrix A corresponding to the linear transformation L can be reduced to a block diagonal matrix under a certain basis
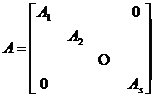
The order in the formula is equal to the dimension of .![]()
![]()
![]()
Second, the standardization of the square matrix
The form of [ Ruodang block and Ruodang standard square matrix ] is
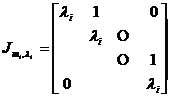
The m -order square matrix of is called the Rodang block, where is an eigenvalue .![]()
The sub-matrix of a block matrix of a square matrix on the main diagonal is a block, and the rest of the sub-matrix are zero matrices, that is,
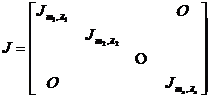 ( 1 )
( 1 )
Then it is called the Rowdang standard square matrix or the Rowdang standard form . Note that these are not necessarily different in different blocks .![]()
[ Standardization of Square Matrix ]
1 o In the case of different eigenvalues If the eigenvalues of a square matrix A are not equal, then A can be transformed into a diagonal matrix,
The elements on its main diagonal are these eigenvalues:

2 o When the eigenvalues are equal, any square matrix A can be transformed into its similar Rowdang standard form ( 1 ), where ![]()
is its eigenvalue and is the multiplicity of eigenvalues . If the order of the blocks is ignored, the canonical form of A is unique .![]()
![]()
![]()
It can be reduced to a diagonal matrix if and only if the order of all the blocks is equal to 1. This is the case of 1 o .![]()
As explained above, assuming that A is a square matrix, then a non-singular square matrix T can always be found , making the square matrix similar to A.![]()
![]()
3. Methods and steps of square matrix standardization
[ λ Matrix ] Assuming that the elements of an n -order square matrix A are all complex coefficient polynomials of variable λ , it is called a λ matrix . The highest order r of a sub-form of a λ matrix that is not equal to zero is called the rank .
![]()
![]()
![]()
![]()
[ Invariant factor and elementary factor ] Let r be the rank, k is a positive integer , and the highest common factor of all k -order sub-formulas of is a polynomial, and the specified coefficient of the highest-order term is 1 ; in addition, it is specified that![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
say
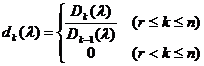
invariant factor for .![]()
Decompose each into a first-order factor, we get![]()
![]()
Some of the exponents in the formula may be zero, and at that time , it is called an elementary factor of .
![]()
![]()
![]()
![]()
[ Elementary Transformation · Matrix Equivalence ] A finite combination of the following three transformations on the λ matrix is called an elementary transformation .![]()
![]()
( i ) any two rows (columns) are interchanged;
( ii ) Multiply each element of any row (column) by the same λ polynomial and add it to the corresponding element of another row (column);
( iii ) Multiply any row (column) element by the same complex number not equal to zero .
It should be noted that, properly implementing ( ii ), ( iii ) both transformations can yield ( i ) .
If it can be obtained by a finite number of elementary transformations, it is said to be equivalent to .![]()
![]()
![]()
![]()
![]()
After the λ matrix undergoes elementary transformation, its invariant factor and elementary factor remain unchanged .
[ Standard form of λ matrix ] Let the rank of the λ matrix be r and the invariant factor be , then ![]()
![]()

Call the square matrix on the right the canonical form . It is determined by unique .![]()
![]()
Equivalent λ matrices have the same canonical form .
[ eigenmatrix ] The eigenmatrix of square matrix A is a special λ matrix . So![]()
1 o If the elementary factor is![]()
![]()
which are not necessarily different from each other, then![]()
![]()
and have
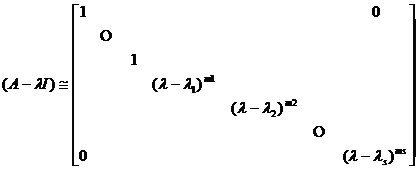
2 o if the nth order λ matrix
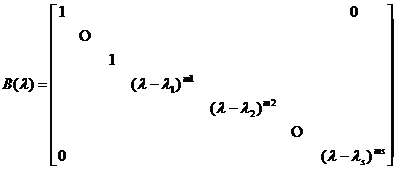
Among them , then![]()
![]()
where J is the standard form of A.
3 o If the elementary factor of the characteristic matrix of A is
![]()
but
![]()
If J is the standard form of A.
[ Steps of Square Matrix Standardization ] The steps to convert the square matrix A into the standard form of A are as follows:
(1) Use elementary transformation to convert it into a diagonal matrix, decompose the polynomial on the diagonal, and get all the elementary factors .
![]()
![]()
(2) Corresponding to each elementary factor , make a m -order Row-Dang block![]()
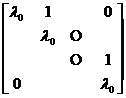
(3) Combine all the Ruodang blocks to get the Ruodang canonical form of A.
Example 1 to find a square matrix
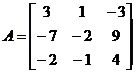
The Jodang standard form of .
untie
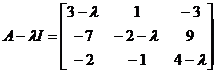
It is easy to find that its invariant factors are 1 , 1 , , so the elementary factors are![]()
![]()
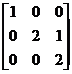
Example 2 Find a square matrix
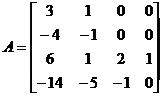
The Jodang standard form of .
untie
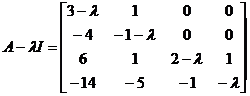
After elementary transformation, it can be transformed into a diagonal matrix of the following form
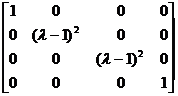
So the elementary factor is , , and the corresponding if-dang block is![]()
![]()
![]()
Therefore , the standard form of A 's jodang is
