A differential equation or system of Ordinary Differential Equations is said to
be autonomous if it does not explicitly contain the independent variable (usually denoted  ). A second-order
autonomous differential equation is of the form
). A second-order
autonomous differential equation is of the form 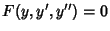 , where
, where
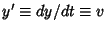 . By the Chain
Rule,
. By the Chain
Rule, 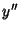 can be expressed as
can be expressed as
For an autonomous ODE, the solution is independent of the time at which the
initial conditions are applied. This means that all particles pass through a given point in phase space. A
nonautonomous system of 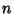 first-order ODEs can be written as an autonomous system of
first-order ODEs can be written as an autonomous system of 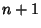 ODEs by letting
ODEs by letting
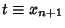 and increasing the dimension of the system by 1 by adding the equation
and increasing the dimension of the system by 1 by adding the equation
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ). A second-order
autonomous differential equation is of the form
). A second-order
autonomous differential equation is of the form ![]() , where
, where
![]() . By the Chain
Rule,
. By the Chain
Rule, ![]() can be expressed as
can be expressed as