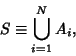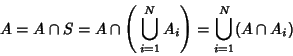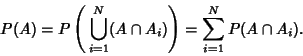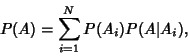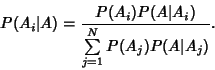Let 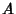 and
and 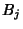 be Sets. Conditional Probability requires that
be Sets. Conditional Probability requires that
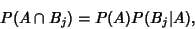 |
(1) |
where 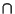 denotes Intersection (``and''), and also that
denotes Intersection (``and''), and also that
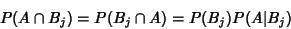 |
(2) |
and
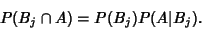 |
(3) |
Since (2) and (3) must be equal,
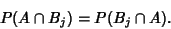 |
(4) |
From (2) and (3),
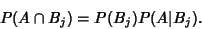 |
(5) |
Equating (5) with (2) gives
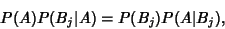 |
(6) |
so
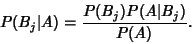 |
(7) |
Now, let
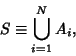 |
(8) |
so 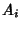 is an event in
is an event in 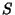 and
and
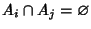 for
for 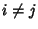 , then
, then
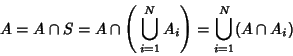 |
(9) |
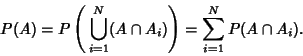 |
(10) |
From (5), this becomes
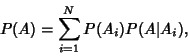 |
(11) |
so
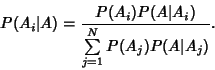 |
(12) |
See also Conditional Probability, Independent Statistics
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, p. 810, 1992.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() be Sets. Conditional Probability requires that
be Sets. Conditional Probability requires that