A mathematical object which is similar to a Boolean Ring, but which uses the meet and join operators instead of the
usual addition and multiplication operators. A Boolean algebra is a set 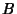 of elements
of elements  ,
, 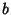 , ... with Binary
Operators
, ... with Binary
Operators 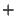 and
and 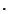 such that
such that
- 1a. If
 and
and 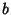 are in the set
are in the set 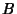 , then
, then 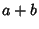 is in the set
is in the set 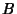 .
.
- 1b. If
 and
and 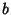 are in the set
are in the set 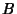 , then
, then 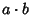 is in the set
is in the set 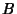 .
.
- 2a. There is an element
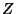 (zero) such that
(zero) such that  for every element
for every element  .
.
- 2b. There is an element
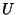 (unity) such that
(unity) such that 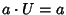 for every element
for every element  .
.
- 3a.
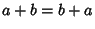
- 3b.

- 4a.
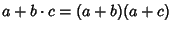
- 4b.
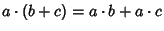
- 5. For every element
 there is an element
there is an element 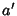 such that
such that 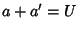 and
and 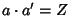 .
.
- 6. There are at least two distinct elements in the set
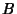 .
.
(Bell 1937, p. 444).
In more modern terms, a Boolean algebra is a Set 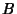 of elements
of elements  ,
, 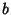 , ... with the following
properties:
, ... with the following
properties:
- 1.
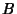 has two binary operations,
has two binary operations, 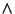 (Wedge) and
(Wedge) and 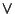 (Vee), which satisfy the
Idempotent laws
(Vee), which satisfy the
Idempotent laws
the Commutative laws
and the Associative laws
- 2. The operations satisfy the Absorption Law
- 3. The operations are mutually distributive
- 4.
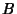 contains universal bounds
contains universal bounds 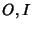 which satisfy
which satisfy
- 5.
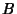 has a unary operation
has a unary operation 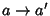 of complementation which obeys the laws
of complementation which obeys the laws
(Birkhoff and Mac Lane 1965). Under intersection, union, and complement, the subsets of any set  form a
Boolean algebra.
form a
Boolean algebra.
Huntington (1933a, b) presented the following basis for Boolean algebra,
- 1. Commutativity.
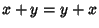 .
.
- 2. Associativity.
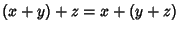 .
.
- 3. Huntington Equation.
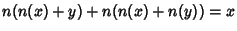 .
.
H. Robbins then conjectured that the Huntington Equation could be replaced with the simpler Robbins Equation,
The Algebra defined by commutativity, associativity, and the Robbins Equation is called Robbins
Algebra. Computer theorem proving demonstrated that every Robbins Algebra satisfies the second Winkler
Condition, from which it follows immediately that all Robbins Algebras are
Boolean.
References
Bell, E. T. Men of Mathematics. New York: Simon and Schuster, 1986.
Birkhoff, G. and Mac Lane, S. A Survey of Modern Algebra, 3rd ed. New York: Macmillian, p. 317, 1965.
Halmos, P. Lectures on Boolean Algebras. Princeton, NJ: Van Nostrand, 1963.
Huntington, E. V. ``New Sets of Independent Postulates for the Algebra of Logic.'' Trans. Amer. Math. Soc.
35, 274-304, 1933a.
Huntington, E. V. ``Boolean Algebras: A Correction.'' Trans. Amer. Math. Soc. 35, 557-558, 1933.
McCune, W. ``Robbins Algebras are Boolean.''
http://www-unix.mcs.anl.gov/~mccune/papers/robbins/.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() of elements
of elements ![]() ,
, ![]() , ... with Binary
Operators
, ... with Binary
Operators ![]() and
and ![]() such that
such that
![]() of elements
of elements ![]() ,
, ![]() , ... with the following
properties:
, ... with the following
properties: