|
|
|
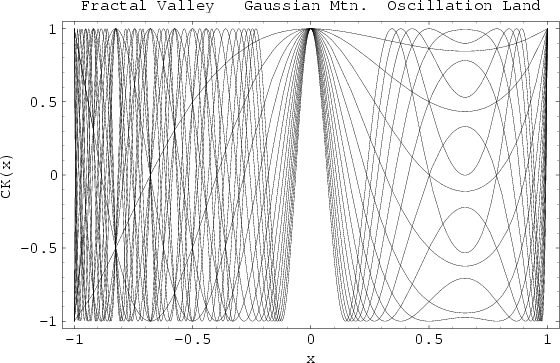
A fractal-like structure is produced for ![]() by superposing plots of Carotid-Kundalini Functions
by superposing plots of Carotid-Kundalini Functions ![]() of different orders
of different orders ![]() . The region
. The region ![]() is called Fractal Land
by Pickover (1995), the central region the Gaussian Mountain Range, and the region
is called Fractal Land
by Pickover (1995), the central region the Gaussian Mountain Range, and the region ![]() Oscillation
Land. The plot above shows
Oscillation
Land. The plot above shows ![]() to 25. Gaps in Fractal Land occur whenever
to 25. Gaps in Fractal Land occur whenever
References
Pickover, C. A. ``Are Infinite Carotid-Kundalini Functions Fractal?''
Ch. 24 in Keys to Infinity. New York: Wiley, pp. 179-181, 1995.