A continuous function is a Function
 where the pre-image of every Open Set in
where the pre-image of every Open Set in 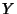 is
Open in
is
Open in 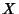 . A function
. A function 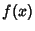 in a single variable
in a single variable  is said to be continuous at point
is said to be continuous at point  if
if
-
- 1.
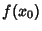 is defined, so that
is defined, so that  is in the Domain of
is in the Domain of 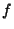 .
.
- 2.
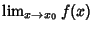 exists for
exists for  in the Domain of
in the Domain of 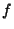 .
.
- 3.
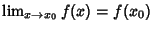 ,
,
where lim denotes a Limit. If 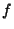 is Differentiable at point
is Differentiable at point  , then it is also continuous at
, then it is also continuous at  . If
. If
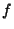 and
and 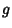 are continuous at
are continuous at  , then
, then
-
- 1.
 is continuous at
is continuous at  .
.
- 2.
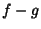 is continuous at
is continuous at  .
.
- 3.
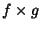 is continuous at
is continuous at  .
.
- 4.
 is continuous at
is continuous at  if
if
 and is discontinuous at
and is discontinuous at  if
if  .
.
- 5.
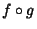 is continuous at
is continuous at  , where
, where 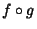 denotes
denotes 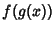 , the Composition of the
functions
, the Composition of the
functions 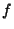 and
and 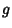 .
.
See also Critical Point, Differentiable, Limit, Neighborhood, Stationary Point
© 1996-9 Eric W. Weisstein
1999-05-26
![]() where the pre-image of every Open Set in
where the pre-image of every Open Set in ![]() is
Open in
is
Open in ![]() . A function
. A function ![]() in a single variable
in a single variable ![]() is said to be continuous at point
is said to be continuous at point ![]() if
if