|
|
|
Define the correlation integral as
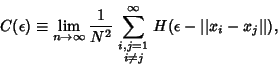 |
(1) |
![\begin{displaymath}
D_2\equiv d_{\rm cor} \equiv \lim_{\epsilon, \epsilon'\to 0^...
...')}
\right]}\over{\ln\left({\epsilon\over\epsilon'}\right)}}.
\end{displaymath}](c3_353.gif) |
(2) |
| (3) |
| (4) |
To estimate the correlation dimension of an ![]() -dimensional system with accuracy
-dimensional system with accuracy ![]() requires
requires ![]() data points, where
data points, where
| (5) |
| (6) |
See also Correlation Exponent, q-Dimension
References
Nayfeh, A. H. and Balachandran, B. Applied Nonlinear Dynamics: Analytical, Computational, and Experimental
Methods. New York: Wiley, pp. 547-548, 1995.