|
|
|
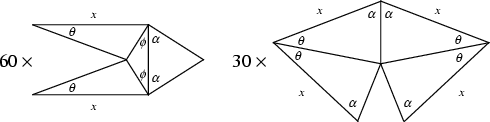
A Polyhedron Compound consisting of the arrangement of five Cubes in the Vertices of a Dodecahedron. In the above figure, let ![]() be the length of a Cube Edge. Then
be the length of a Cube Edge. Then
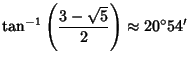 |
|||
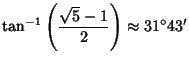 |
|||
See also Cube, Cube 2-Compound, Cube 3-Compound, Cube 4-Compound, Dodecahedron, Polyhedron Compound, Rhombic Triacontahedron
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York:
Dover, pp. 135 and 137, 1987.
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 135-136, 1989.