Given a Matrix
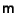 , the following are equivalent:
, the following are equivalent:
- 1.
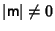 .
.
- 2. The columns of m are linearly independent.
- 3. The rows of m are linearly independent.
- 4. Range(m) =
 .
.
- 5. Null(m) =
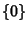 .
.
- 6. m has a Matrix Inverse.
See also Determinant, Matrix Inverse, Nullspace, Range (Image)
© 1996-9 Eric W. Weisstein
1999-05-24
![]() , the following are equivalent:
, the following are equivalent: