|
|
|
A Tensor ![]() is said to satisfy the double contraction relation when
is said to satisfy the double contraction relation when
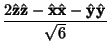 |
|||
See also Spherical Harmonic Tensor, Tensor
References
Arfken, G. ``Alternating Series.'' Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, p. 140, 1985.