A differential of the form
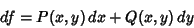 |
(1) |
is exact (also called a Total Differential) if 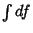 is path-independent. This will be true if
is path-independent. This will be true if
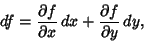 |
(2) |
so 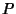 and
and 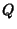 must be of the form
must be of the form
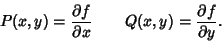 |
(3) |
But
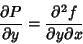 |
(4) |
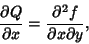 |
(5) |
so
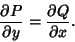 |
(6) |
See also Pfaffian Form, Inexact Differential
© 1996-9 Eric W. Weisstein
1999-05-25