For one discrete variable,
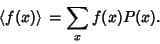 |
(1) |
For one continuous variable,
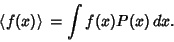 |
(2) |
The expectation value satisfies
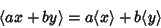 |
(3) |
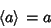 |
(4) |
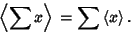 |
(5) |
For multiple discrete variables
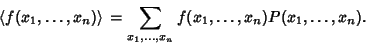 |
(6) |
For multiple continuous variables
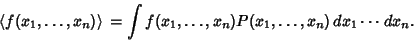 |
(7) |
The (multiple) expectation value satisfies
where 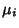 is the Mean for the variable
is the Mean for the variable  .
.
See also Mean
© 1996-9 Eric W. Weisstein
1999-05-25