|
|
|
A formula for Numerical Integration,
|
|
|
|
|
(1) |
![$\displaystyle \sum_{i=0}^n f_{2i}\cos(tx_{2i})-{\textstyle{1\over 2}}[f_{2n}\cos(tx_{2n})+f_0\cos(tx_0)]$](f_985.gif) |
|||
| (2) | |||
 |
(3) | ||
 |
(4) | ||
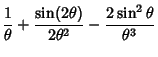 |
(5) | ||
![$\displaystyle 2\left[{{1+\cos^2\theta\over\theta^2}-{\sin(2\theta)\over\theta^3}}\right]$](f_993.gif) |
(6) | ||
 |
(7) |
| (8) |
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 890-891, 1972.
Tukey, J. W. In On Numerical Approximation: Proceedings of a Symposium Conducted by the Mathematics
Research Center, United States Army, at the University of Wisconsin, Madison, April 21-23, 1958
(Ed. R. E. Langer). Madison, WI: University of Wisconsin Press, p. 400, 1959.