Let
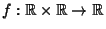 be a one-parameter family of
be a one-parameter family of 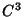 maps satisfying
maps satisfying
Then there are intervals 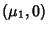 ,
,  , and
, and 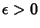 such that
such that
- 1. If
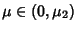 , then
, then 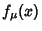 has one unstable fixed point and one stable orbit of period two for
has one unstable fixed point and one stable orbit of period two for
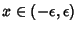 , and
, and
- 2. If
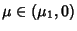 , then
, then 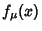 has a single stable fixed point for
has a single stable fixed point for
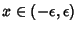 .
.
This type of Bifurcation is known as a flip bifurcation. An example of an equation displaying a flip bifurcation is
See also Bifurcation
References
Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 27-30, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be a one-parameter family of
be a one-parameter family of ![]() maps satisfying
maps satisfying
![$\displaystyle \left[{\partial f\over\partial x}\right]_{\mu=0, x=0}$](f_1463.gif)
![$\displaystyle \left[{\partial^2 f\over\partial x^2}\right]_{\mu=0, x=0}$](f_1464.gif)
![$\displaystyle \left[{\partial^3 f\over\partial x^3}\right]_{\mu=0, x=0}$](f_1466.gif)