Define
where 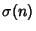 is the Divisor Function. Then a Pair of distinct numbers
is the Divisor Function. Then a Pair of distinct numbers  is a friendly pair
(and
is a friendly pair
(and  is said to be a Friend of
is said to be a Friend of  ) if
) if
For example, 4320 and 4680 are a friendly pair, since
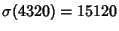 ,
,
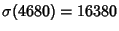 , and
, and
Numbers which do not have Friends are called Solitary Numbers.
Solitary Numbers satisfy
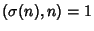 , where
, where 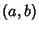 is the Greatest Common Divisor
of
is the Greatest Common Divisor
of 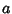 and
and 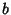 .
.
See also Aliquot Sequence, Friend, Solitary Number
References
Anderson, C. W. and Hickerson, D. Problem 6020. ``Friendly Integers.'' Amer. Math. Monthly 84,
65-66, 1977.
© 1996-9 Eric W. Weisstein
1999-05-26