Full Width at Half Maximum

The full width at half maximum (FWHM) is a parameter commonly used to describe the width of a ``bump'' on a curve or function. It is given by the distance between points on the curve at which the function reaches half its maximum value. The following table gives analytic and numerical full widths for several common curves.

Function	Formula	FWHM
Bartlett	$1-{\vert x\vert\over a}$	$a$
Blackman		$0.810957a$
Connes	$\left({1-{x^2\over a^2}}\right)$	$\sqrt{4-2\sqrt{2}}\,a$
Cosine	$\cos\left({\pi x\over 2a}\right)$	${\textstyle{4\over 3}}a$
Gaussian	$e^{-x^2/(2\sigma^2)}$	$2\sqrt{2\ln 2}\,\sigma$
Hamming		$1.05543a$
Hanning		$a$
Lorentzian	${{\textstyle{1\over 2}}\Gamma\over x^2+({\textstyle{1\over 2}}\Gamma)^2}$	$\Gamma$
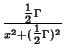Welch	$1-{x^2\over a^2}$	$\sqrt{2}\,a$

See also Apodization Function, Maximum