|
|
|
A geometric series ![]() is a series for which the ratio of each two consecutive terms
is a series for which the ratio of each two consecutive terms ![]() is a constant
function of the summation index
is a constant
function of the summation index ![]() , say
, say ![]() . Then the terms
. Then the terms ![]() are of the form
are of the form ![]() , so
, so ![]() . If
. If
![]() , with
, with ![]() , 2, ..., is a Geometric Sequence with multiplier
, 2, ..., is a Geometric Sequence with multiplier ![]() and
and ![]() , then the geometric
series
, then the geometric
series
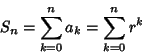 |
(1) |
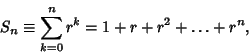 |
(2) |
| (3) |
| (4) |
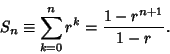 |
(5) |
 |
(6) |
See also Arithmetic Series, Gabriel's Staircase, Harmonic Series, Hypergeometric Series, Wheat and Chessboard Problem
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 10, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 278-279, 1985.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 8, 1987.
Courant, R. and Robbins, H. ``The Geometric Progression.'' §1.2.3 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 13-14, 1996.
Pappas, T. ``Perimeter, Area & the Infinite Series.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 134-135, 1989.
|
|
|
© 1996-9 Eric W. Weisstein