A 2-D piecewise linear Map defined by
The map is chaotic in the filled region above and stable in the six hexagonal regions. Each point in the interior hexagon
defined by the vertices (0, 0), (1, 0), (2, 1), (2, 2), (1, 2), and (0, 1) has an orbit with period six (except the point
(1, 1), which has period 1). Orbits in the other
five hexagonal regions circulate from one to the other. There is a unique orbit of period five, with all others having period
30. The points having orbits of period five are (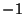 , 3), (
, 3), (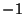 ,
, 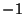 ), (3,
), (3, 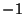 ), (5, 3), and (3, 5), indicated in the
above figure by the black line. However, there are infinitely many distinct periodic orbits which have an arbitrarily long
period.
), (5, 3), and (3, 5), indicated in the
above figure by the black line. However, there are infinitely many distinct periodic orbits which have an arbitrarily long
period.
References
Devaney, R. L. ``A Piecewise Linear Model for the Zones of Instability of an Area Preserving Map.'' Physica D 10, 387-393, 1984.
Peitgen, H.-O. and Saupe, D. (Eds.). ``A Chaotic Gingerbreadman.'' §3.2.3 in
The Science of Fractal Images. New York: Springer-Verlag, pp. 149-150, 1988.
© 1996-9 Eric W. Weisstein
1999-05-25
