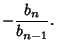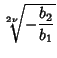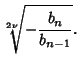A Root-finding method which proceeds by multiplying a Polynomial 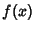 by
by 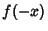 and noting that
and noting that
so the result is
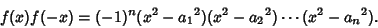 |
(3) |
Repeat 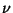 times, then write this in the form
times, then write this in the form
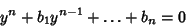 |
(4) |
where
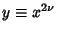 . Since the coefficients are given by Newton's Relations
. Since the coefficients are given by Newton's Relations
and since the squaring procedure has separated the roots, the first term is larger than rest. Therefore,
giving
Solving for the original roots gives
This method works especially well if all roots are real.
References
von Kármán, T. and Biot, M. A. ``Squaring the Roots (Graeffe's Method).'' §5.8.c in
Mathematical Methods in Engineering: An Introduction to the Mathematical Treatment of Engineering Problems.
New York: McGraw-Hill, pp. 194-196, 1940.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() by
by ![]() and noting that
and noting that