Also known as the Tangent Hyperbolas Method or Halley's Rational Formula. As in Halley's Irrational
Formula, take the second-order Taylor Polynomial
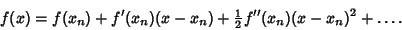 |
(1) |
A Root of  satisfies
satisfies 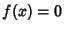 , so
, so
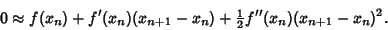 |
(2) |
Now write
![\begin{displaymath}
0=f(x_n)+(x_{n+1}-x_n)[f'(x_n)+{\textstyle{1\over 2}}f''(x_n)(x_{n+1}-x_n)],
\end{displaymath}](h_172.gif) |
(3) |
giving
 |
(4) |
Using the result from Newton's Method,
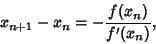 |
(5) |
gives
![\begin{displaymath}
x_{n+1}=x_n-{2f(x_n)f'(x_n)\over 2[f'(x_n)]^2-f(x_n)f''(x_n)},
\end{displaymath}](h_175.gif) |
(6) |
so the iteration function is
![\begin{displaymath}
H_f(x)=x-{2f(x)f'(x)\over 2[f'(x)]^2-f(x)f''(x)}.
\end{displaymath}](h_176.gif) |
(7) |
This satisfies
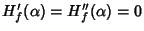 where
where 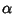 is a Root, so it is third order for simple zeros.
Curiously, the third derivative
is a Root, so it is third order for simple zeros.
Curiously, the third derivative
![\begin{displaymath}
H_f'''(\alpha)=-\left\{{{f'''(\alpha)\over f'(\alpha)}-{3\over 2}\left[{f''(\alpha)\over f'(\alpha)}\right]^2}\right\}
\end{displaymath}](h_179.gif) |
(8) |
is the Schwarzian Derivative. Halley's method may also be derived by applying Newton's Method to
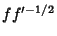 . It may also be derived by using an Osculating Curve of the form
. It may also be derived by using an Osculating Curve of the form
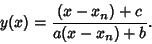 |
(9) |
Taking derivatives,
which has solutions
so at a Root, 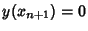 and
and
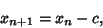 |
(16) |
which is Halley's method.
See also Halley's Irrational Formula, Laguerre's Method, Newton's Method
References
Scavo, T. R. and Thoo, J. B. ``On the Geometry of Halley's Method.'' Amer. Math. Monthly 102,
417-426, 1995.
© 1996-9 Eric W. Weisstein
1999-05-25
![\begin{displaymath}
H_f'''(\alpha)=-\left\{{{f'''(\alpha)\over f'(\alpha)}-{3\over 2}\left[{f''(\alpha)\over f'(\alpha)}\right]^2}\right\}
\end{displaymath}](h_179.gif)
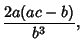
![$\displaystyle -{f''(x_n)\over 2[f'(x_n)]^2-f(x_n)f''(x_n)}$](h_189.gif)
![$\displaystyle {2f'(x_n)\over 2[f'(x_n)]^2-f(x_n)f''(x_n)}$](h_191.gif)
![$\displaystyle {2f(x_n)f'(x_n)\over 2[f'(x_n)]^2-f(x_n)f''(x_n)},$](h_193.gif)