Describe subsets of elements 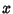 in a Neighborhood Set
in a Neighborhood Set 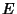 of
of 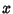 . The Neighborhood is assumed to
satisfy:
. The Neighborhood is assumed to
satisfy:
- 1. There corresponds to each point
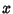 at least one Neighborhood
at least one Neighborhood 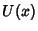 , and each Neighborhood
, and each Neighborhood 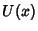 contains the point
contains the point 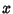 .
.
- 2. If
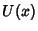 and
and 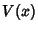 are two Neighborhoods of the same point
are two Neighborhoods of the same point 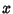 , there must exist a
Neighborhood
, there must exist a
Neighborhood 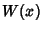 that is a subset of both.
that is a subset of both.
- 3. If the point
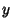 lies in
lies in 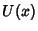 , there must exist a Neighborhood
, there must exist a Neighborhood 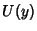 that is a Subset of
that is a Subset of
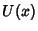 .
.
- 4. For two different points
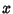 and
and 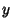 , there are two corresponding Neighborhoods
, there are two corresponding Neighborhoods 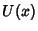 and
and
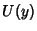 with no points in common.
with no points in common.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() in a Neighborhood Set
in a Neighborhood Set ![]() of
of ![]() . The Neighborhood is assumed to
satisfy:
. The Neighborhood is assumed to
satisfy: