A method for finding roots of a polynomial equation 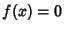 by finding an equation whose roots are the same, but
diminished by
by finding an equation whose roots are the same, but
diminished by 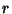 , so
, so
The expressions for 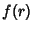 ,
, 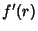 , ... are then found by writing the coefficients
, ... are then found by writing the coefficients 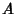 ,
, 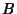 , ...,
, ..., 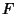 in a horizontal
row, and letting a new letter shown as a denominator stand for the sum immediately above it. To find a root, first determine
the integer part of the root through whatever means are needed, then reduce the equation by this amount. This gives the second
digit, by which the equation is once again reduced (after suitable multiplication by 10) to find the third digit, and so on.
Horner's process really boils down to the construction of a Divided Difference table.
in a horizontal
row, and letting a new letter shown as a denominator stand for the sum immediately above it. To find a root, first determine
the integer part of the root through whatever means are needed, then reduce the equation by this amount. This gives the second
digit, by which the equation is once again reduced (after suitable multiplication by 10) to find the third digit, and so on.
Horner's process really boils down to the construction of a Divided Difference table.
See also Newton's Method
© 1996-9 Eric W. Weisstein
1999-05-25
![]() by finding an equation whose roots are the same, but
diminished by
by finding an equation whose roots are the same, but
diminished by ![]() , so
, so