|
|
|
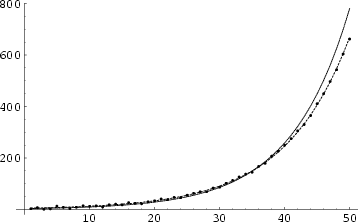
To fit a functional form
| (1) |
| (2) |
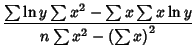 |
(3) | ||
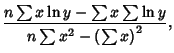 |
(4) |
This fit gives greater weights to small ![]() values so, in order to weight the points equally, it is often better to
minimize the function
values so, in order to weight the points equally, it is often better to
minimize the function
| (5) |
| (6) |
| (7) |
| (8) |
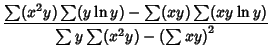 |
(9) | ||
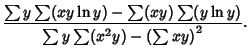 |
(10) |
See also Least Squares Fitting, Least Squares Fitting--Logarithmic, Least Squares Fitting--Power Law