|
|
|
A Fredholm Integral Equation of the Second Kind
| (1) |
| (2) | |||
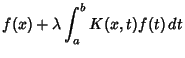 |
(3) | ||
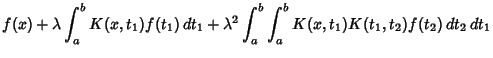 |
(4) | ||
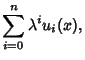 |
(5) |
| (6) | |||
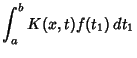 |
(7) | ||
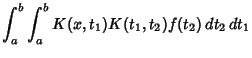 |
(8) | ||
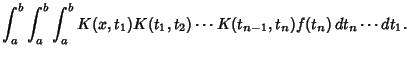 |
(9) |
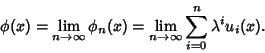 |
(10) |
References
Arfken, G. ``Neumann Series, Separable (Degenerate) Kernels.'' §16.3 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 879-890, 1985.