|
|
|
In informal usage, an ordinal number is an adjective which describes the numerical position of an object, e.g., first, second, third, etc.
In technical mathematics, an ordinal number is one of the numbers in Georg Cantor's ![]() extension of
the Whole Numbers. The ordinal numbers are 0, 1, 2, ...,
extension of
the Whole Numbers. The ordinal numbers are 0, 1, 2, ..., ![]() ,
, ![]() ,
, ![]() , ...,
, ...,
![]() ,
,
![]() , .... Cantor's ``smallest'' Transfinite Number
, .... Cantor's ``smallest'' Transfinite Number ![]() is defined to be the
earliest number greater than all Whole Numbers, and is denoted by Conway and Guy (1996) as
is defined to be the
earliest number greater than all Whole Numbers, and is denoted by Conway and Guy (1996) as
![]() . The notation of ordinal numbers can be a bit counterintuitive, e.g., even though
. The notation of ordinal numbers can be a bit counterintuitive, e.g., even though
![]() ,
,
![]() .
.
Ordinal numbers have some other rather peculiar properties. The sum of two ordinal numbers can take on two different values,
the sum of three can take on five values. The first few terms of this sequence are 2, 5, 13, 33, 81, 193, 449, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , ... (Conway and Guy 1996, Sloane's A005348). The sum of
, ... (Conway and Guy 1996, Sloane's A005348). The sum of ![]() ordinals has
either
ordinals has
either ![]() or
or ![]() possible answers for
possible answers for ![]() (Conway and Guy 1996).
(Conway and Guy 1996).
![]() is the same as
is the same as ![]() , but
, but
![]() is equal to
is equal to
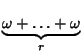 .
.
![]() is larger than any number of the form
is larger than any number of the form
![]() ,
, ![]() is larger than
is larger than ![]() , and so on.
, and so on.
There exist ordinal numbers which cannot be constructed from smaller ones by finite additions, multiplications, and
exponentiations. These ordinals obey Cantor's Equation. The first such ordinal is
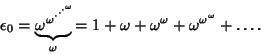
See also Axiom of Choice, Cantor's Equation, Cardinal Number, Order Statistic, Power Set, Surreal Number
References
Cantor, G. Über unendliche, lineare Punktmannigfältigkeiten, Arbeiten zur Mengenlehre aus dem Jahren 1872-1884.
Leipzig, Germany: Teubner-Archiv zur Mathematik, 1884.
Conway, J. H. and Guy, R. K. ``Cantor's Ordinal Numbers.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 266-267 and 274, 1996.
Sloane, N. J. A. Sequence
A005348/M1435
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein