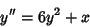 |
(1) |
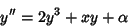 |
(2) |
 |
(3) |
Transcendents 4-6 do not have known first integrals, but all transcendents have first integrals for special values of their
parameters except (1). Painlevé  found the above transcendents (1) to (3), and
the rest were investigated by his students. The sixth transcendent was found by Gambier and contains the other five as
limiting cases.
found the above transcendents (1) to (3), and
the rest were investigated by his students. The sixth transcendent was found by Gambier and contains the other five as
limiting cases.
See also Painlevé Property
© 1996-9 Eric W. Weisstein
1999-05-26