|
|
|
Given two paired sets ![]() and
and ![]() of
of ![]() measured values, the paired
measured values, the paired ![]() -test determines if they differ from each other in
a significant way. Let
-test determines if they differ from each other in
a significant way. Let
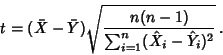
A table of Student's t-Distribution confidence interval can be used to determine the significance level at which two distributions differ.
See also Fisher Sign Test, Hypothesis Testing, Student's t-Distribution, Wilcoxon Signed Rank Test
References
Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, pp. 50-55, 1956.