|
|
|
In a normal ![]() Latin Square, the entries in each row and column are chosen from a ``global'' set of
Latin Square, the entries in each row and column are chosen from a ``global'' set of ![]() objects. Like a Latin square, a partial Latin square has no two rows or columns which contain the same two symbols.
However, in a partial Latin square, each cell is assigned one of its own set of
objects. Like a Latin square, a partial Latin square has no two rows or columns which contain the same two symbols.
However, in a partial Latin square, each cell is assigned one of its own set of ![]() possible ``local'' (and distinct)
symbols, chosen from an overall set of more than three distinct symbols, and these symbols may vary from location to location.
For example, given the possible symbols
possible ``local'' (and distinct)
symbols, chosen from an overall set of more than three distinct symbols, and these symbols may vary from location to location.
For example, given the possible symbols ![]() 1, 2, ..., 6
1, 2, ..., 6![]() which must be arranged as
which must be arranged as
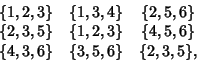
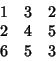
See also Dinitz Problem, Latin Square
References
Cipra, B. ``Quite Easily Done.'' In What's Happening in the Mathematical Sciences 2, pp. 41-46, 1994.