 |
(1) |
where
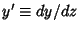 . The transformation
. The transformation
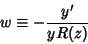 |
(2) |
leads to the second-order linear homogeneous equation
![\begin{displaymath}
R(z)y''-[R'(z)+Q(z)R(z)]y'+[R(z)]^2P(z)y = 0.
\end{displaymath}](r_1402.gif) |
(3) |
Another equation sometimes called the Riccati differential equation is
![\begin{displaymath}
z^2w''+[z^2-n(n+1)]w=0,
\end{displaymath}](r_1403.gif) |
(4) |
which has solutions
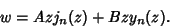 |
(5) |
Yet another form of ``the'' Riccati differential equation is
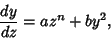 |
(6) |
which is solvable by algebraic, exponential, and logarithmic functions only when
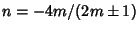 , for
, for  ,
1, 2, ....
,
1, 2, ....
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Riccati-Bessel Functions.''
§10.3 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 445, 1972.
Glaisher, J. W. L. ``On Riccati's Equation.'' Quart. J. Pure Appl. Math. 11, 267-273, 1871.
© 1996-9 Eric W. Weisstein
1999-05-25