Let 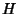 be a 2-D distribution function with marginal distribution functions
be a 2-D distribution function with marginal distribution functions 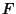 and
and 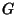 . Then there exists a Copula
. Then there exists a Copula 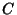 such that
such that
Conversely, for any univariate distribution functions 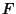 and
and 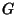 and any Copula
and any Copula 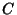 , the function
, the function 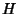 is a
two-dimensional distribution function with marginals
is a
two-dimensional distribution function with marginals 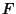 and
and 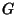 . Furthermore, if
. Furthermore, if 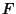 and
and 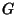 are continuous, then
are continuous, then 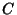 is
unique.
is
unique.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be a 2-D distribution function with marginal distribution functions
be a 2-D distribution function with marginal distribution functions ![]() and
and ![]() . Then there exists a Copula
. Then there exists a Copula ![]() such that
such that