|
|
|
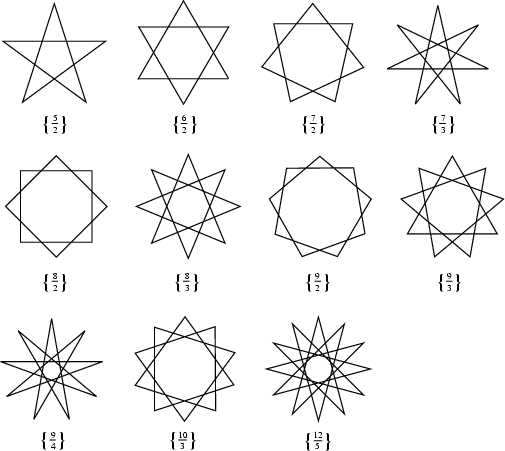
A star polygon ![]() , with
, with ![]() Positive Integers, is a figure formed by connecting with straight
lines every
Positive Integers, is a figure formed by connecting with straight
lines every ![]() th point out of
th point out of ![]() regularly spaced points lying on a Circumference. The number
regularly spaced points lying on a Circumference. The number ![]() is called the
Density of the star polygon. Without loss of generality, take
is called the
Density of the star polygon. Without loss of generality, take ![]() .
.
The usual definition (Coxeter 1969) requires ![]() and
and ![]() to be Relatively Prime. However, the star
polygon can also be generalized to the Star Figure (or ``improper'' star polygon) when
to be Relatively Prime. However, the star
polygon can also be generalized to the Star Figure (or ``improper'' star polygon) when ![]() and
and ![]() share
a common divisor (Savio and Suryanaroyan 1993). For such a figure, if all points are not connected after the
first pass, i.e., if
share
a common divisor (Savio and Suryanaroyan 1993). For such a figure, if all points are not connected after the
first pass, i.e., if ![]() , then start with the first unconnected point and repeat the procedure.
Repeat until all points are connected. For
, then start with the first unconnected point and repeat the procedure.
Repeat until all points are connected. For ![]() , the
, the ![]() symbol can be factored as
symbol can be factored as
| (1) |
| (2) | |||
| (3) |
If ![]() , a Regular Polygon
, a Regular Polygon ![]() is obtained. Special cases of
is obtained. Special cases of ![]() include
include ![]() (the Pentagram),
(the Pentagram),
![]() (the Hexagram, or Star of David),
(the Hexagram, or Star of David), ![]() (the Star of Lakshmi),
(the Star of Lakshmi), ![]() (the
Octagram),
(the
Octagram), ![]() (the Decagram), and
(the Decagram), and ![]() (the Dodecagram).
(the Dodecagram).
The star polygons were first systematically studied by Thomas Bradwardine. ![]()
See also Decagram, Hexagram, Nonagram, Octagram, Pentagram, Regular Polygon, Star of Lakshmi, Stellated Polyhedron
References
Coxeter, H. S. M. ``Star Polygons.'' §2.8 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 36-38, 1969.
Frederickson, G. ``Stardom.'' Ch. 16 in Dissections: Plane and Fancy. New York: Cambridge University Press,
pp. 172-186, 1997.
Savio, D. Y. and Suryanaroyan, E. R. ``Chebyshev Polynomials and Regular Polygons.'' Amer. Math. Monthly 100, 657-661, 1993.
|
|
|
© 1996-9 Eric W. Weisstein